题目内容
计算下列式子
(1)(
+
)÷
;
(2)
(sinx+cosx)dx.
(1)(
| C | 2 100 |
| C | 97 100 |
| A | 3 101 |
(2)
| ∫ | π -π |
考点:定积分,组合及组合数公式
专题:排列组合
分析:(1)利用公式
=
以及
+
=
对括号里化简计算;
(2)直接根据定积分的定义求解即可.
| C | m n |
| C | n-m n |
| C | m n |
| C | m-1 n |
| C | m n+1 |
(2)直接根据定积分的定义求解即可.
解答:
解:(1)原式=(
+
)÷
=
÷
=
=
;
(2)∵∫
(sinx+cosx)dx
=(-cosx+sinx)|
=(-cosπ+sinπ)-[-cos(-π)+sin(π)]
=0.
| C | 2 100 |
| C | 3 100 |
| A | 3 101 |
| C | 3 101 |
| A | 3 101 |
| 1 | ||
|
| 1 |
| 6 |
(2)∵∫
π -π |
=(-cosx+sinx)|
π -π |
=(-cosπ+sinπ)-[-cos(-π)+sin(π)]
=0.
点评:本题考查了组合数公式以及定积分的计算,只要熟记公式,本题不难解决.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
函数f(x)=
,则f(0)=( )
| x+2 |
| A、2 | ||
| B、4 | ||
| C、0 | ||
D、
|
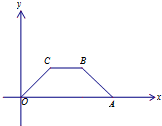 如图所示,四边形OABC是上底为1,下底为3,底角为45°的等腰梯形,由斜二测画法,画出这个梯形的直观图O′A′B′C′,在直观图中的梯形的高为( )
如图所示,四边形OABC是上底为1,下底为3,底角为45°的等腰梯形,由斜二测画法,画出这个梯形的直观图O′A′B′C′,在直观图中的梯形的高为( )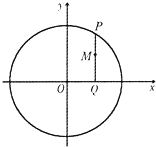 如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a
如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a