题目内容
已知函数f(x)=xlnx,g(x)=2x-3
(1)证明:f(x)>g(x);
(2)证明:(1+1×2)(1+2×3)…(1+2014×2015)>e2×2014-3.
(1)证明:f(x)>g(x);
(2)证明:(1+1×2)(1+2×3)…(1+2014×2015)>e2×2014-3.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)构造函数F(x)=f(x)-g(x),利用导数求出函数的最小值为3-e,问题得证.
(2)由题意得得lnx>
=2-
,令x=1+n(n+1),利用放缩法加以证明.
(2)由题意得得lnx>
| 2x-3 |
| x |
| 3 |
| x |
解答:
证明:(1)令F(x)=f(x)-g(x)=xlnx-2x+3,(x>0)
∴F'(x)=lnx+1-2=lnx-1,
令F'(x)=0,解得x=e,
∴x∈(0,e),F'(x)<0,
x∈(e,+∞),F'(x)>0,
∴当x=e时函数F(x)有最小值,即为F(e)=elne-2e+3=3-e>0,
故f(x)>g(x).
(2)由(1)xlnx>2x-3,
得lnx>
=2-
,
令x=1+n(n+1),
故ln[1+n(n+1)]>2-
>2-
,
∴ln(1+1×2)+ln(1+2×3)+…+ln(1+2014×2015)>2×2014-3[
+
+…+
]=2×2014-3[1-
]>2×2014-3
即ln[(1+1×2)(1+2×3)…(1+2014×2015)]>2×2014-3
则(1+1×2)(1+2×3)…(1+2014×2015)>e2×2014-3成立.
故问题得以证明.
∴F'(x)=lnx+1-2=lnx-1,
令F'(x)=0,解得x=e,
∴x∈(0,e),F'(x)<0,
x∈(e,+∞),F'(x)>0,
∴当x=e时函数F(x)有最小值,即为F(e)=elne-2e+3=3-e>0,
故f(x)>g(x).
(2)由(1)xlnx>2x-3,
得lnx>
| 2x-3 |
| x |
| 3 |
| x |
令x=1+n(n+1),
故ln[1+n(n+1)]>2-
| 3 |
| 1+n(n+1) |
| 3 |
| n(n+1) |
∴ln(1+1×2)+ln(1+2×3)+…+ln(1+2014×2015)>2×2014-3[
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2014×2015 |
| 1 |
| 2015 |
即ln[(1+1×2)(1+2×3)…(1+2014×2015)]>2×2014-3
则(1+1×2)(1+2×3)…(1+2014×2015)>e2×2014-3成立.
故问题得以证明.
点评:本题主要考查了导数以函数的最值的关系,以及利用放缩法证明不等式成立的问题,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
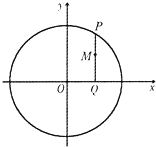 如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a
如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a