题目内容
已知100m=5,10n=2,
(1)求2m+n的值.
(2)x1、x2、…x2013均为正实数,若函数f(x)=logax(a>0且a≠1)且f(x1x2…x2013)=2m+n,求f(x12)+f(x22)+…+f(x20132)的值.
(1)求2m+n的值.
(2)x1、x2、…x2013均为正实数,若函数f(x)=logax(a>0且a≠1)且f(x1x2…x2013)=2m+n,求f(x12)+f(x22)+…+f(x20132)的值.
考点:对数的运算性质
专题:函数的性质及应用
分析:(1)由100m=102m=5,得102m•10n=102m+n=5•2=10,由此能求出2m+n=1.
(2)由(1)知f(x1x2…x2013)=f(x1)+f(x2)+…+f(2013)=1,能此利用对数性质能求出f(x12)+f(x22)+…+f(x20132)的值.
(2)由(1)知f(x1x2…x2013)=f(x1)+f(x2)+…+f(2013)=1,能此利用对数性质能求出f(x12)+f(x22)+…+f(x20132)的值.
解答:
解:(1)∵100m=102m=5,…(2分)
∴102m•10n=102m+n=5•2=10,…(4分)
∴2m+n=1.…(5分)
(2)由(1)知f(x1x2…x2013)=f(x1)+f(x2)+…+f(2013)=1,…(7分)
∴f(x12)+f(x22)+…+f(x20132)
=2[f(x1)+f(x2)+…+f(x2013)]…(9分)
=2×1=2.…(10分)
∴102m•10n=102m+n=5•2=10,…(4分)
∴2m+n=1.…(5分)
(2)由(1)知f(x1x2…x2013)=f(x1)+f(x2)+…+f(2013)=1,…(7分)
∴f(x12)+f(x22)+…+f(x20132)
=2[f(x1)+f(x2)+…+f(x2013)]…(9分)
=2×1=2.…(10分)
点评:本题考查代数式的值的求法,考查函数值的求法,解题时要认真审题,注意对数性质的合理运用.

练习册系列答案
相关题目
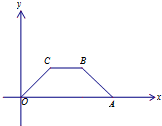 如图所示,四边形OABC是上底为1,下底为3,底角为45°的等腰梯形,由斜二测画法,画出这个梯形的直观图O′A′B′C′,在直观图中的梯形的高为( )
如图所示,四边形OABC是上底为1,下底为3,底角为45°的等腰梯形,由斜二测画法,画出这个梯形的直观图O′A′B′C′,在直观图中的梯形的高为( )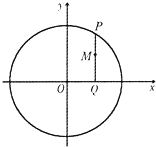 如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a
如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a