题目内容
已知直线m:(a+2)x+(1-2a)y+4-3a=0.
(1)求证直线m过定点M;
(2)过点M作直线n使直线与两负半轴围成的三角形AOB的面积等于4,求直线n的方程.
(1)求证直线m过定点M;
(2)过点M作直线n使直线与两负半轴围成的三角形AOB的面积等于4,求直线n的方程.
考点:恒过定点的直线,直线的截距式方程
专题:直线与圆
分析:(1)按照字母a集项,利用直线系方程,解方程组求出定点,说明直线m过定点M;
(2)设出截距式方程,利用过点M作直线n使直线与两负半轴围成的三角形AOB的面积等于4,得到方程组,即可求直线n的方程.
(2)设出截距式方程,利用过点M作直线n使直线与两负半轴围成的三角形AOB的面积等于4,得到方程组,即可求直线n的方程.
解答:
解:(1)方程m:(a+2)x+(1-2a)y+4-3a=0可化为a(x-2y-3)+(2x+y+4)=0,
要使a有无穷多个解,必须有
,得
.
无论a取何值,(-1,-2)都满足方程,故直线m过定点M(-1,-2).
(2)设直线n:
+
=1,
则
,解得
,故直线n:
+
=1,
所以当直线n为2x+y+4=0时,三角形的面积为4.
要使a有无穷多个解,必须有
|
|
无论a取何值,(-1,-2)都满足方程,故直线m过定点M(-1,-2).
(2)设直线n:
| x |
| a |
| y |
| b |
则
|
|
| x |
| -2 |
| y |
| -4 |
所以当直线n为2x+y+4=0时,三角形的面积为4.
点评:本题考查直线方程的应用,截距式方程的应用,基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
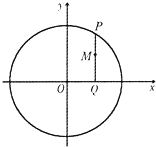 如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a
如图,设P是圆O:x2+y2=a2上的任意一点,过点P与x轴垂直的直线与x轴交于点Q,点M满足a