题目内容
下列说法正确的是( )
A、函数y=
| ||
| B、根据函数定义,函数在不同定义域上,值域也应不同 | ||
| C、空集是任何集合的子集,但是空集没有子集 | ||
| D、函数的单调区间一定是其定义域的一个子集 |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据反比例函数的单调性,定义域、值域的关系,任何集合和自身的关系,和单调性的定义即可找出正确说法.
解答:
解:A.错误,y=
是反比例函数,在定义域内不具有单调性;
B.错误,不一定,比如y=x2,在不同定义域(0,+∞)和(-∞,0)上的值域相同为(0,+∞);
C.错误,任何集合是自身的子集,所以空集是自身的子集,即空集有子集;
D.正确,根据单调性的定义,单调区间是定义在定义域上的,所以是定义域的一个子集.
故选D.
| 1 |
| x |
B.错误,不一定,比如y=x2,在不同定义域(0,+∞)和(-∞,0)上的值域相同为(0,+∞);
C.错误,任何集合是自身的子集,所以空集是自身的子集,即空集有子集;
D.正确,根据单调性的定义,单调区间是定义在定义域上的,所以是定义域的一个子集.
故选D.
点评:考查反比例函数的单调性,函数定义域和值域的关系,子集的概念,以及单调性的定义.

练习册系列答案
相关题目
函数y=
的定义域是( )
| ||
| x-2 |
A、[
| ||
B、[
| ||
C、(
| ||
| D、(-∞,2)∪(2,+∞) |
已知函数f(x)=loga(ax2-x+3)在[2,4]上是增函数,则实数a的取值范围是( )
| A、a>1 | ||||
| B、0<a<1或a>1 | ||||
C、
| ||||
D、
|
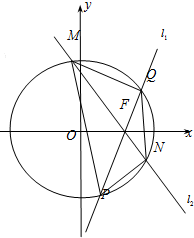 已知椭圆
已知椭圆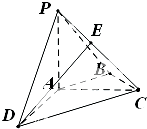 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AB=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AB=