题目内容
已知椭圆
+
=1，则以点M（-1，2）为中点的弦所在直线方程为（ ）
| x2 |
| 12 |
| y2 |
| 16 |
| A、3x-8y+19=0 |
| B、3x+8y-13=0 |
| C、2x-3y+8=0 |
| D、2x+3y-4=0 |
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：利用点差法求解．
解答：
解：设以M（-1，2）为中点的弦与椭圆
+
=1交于点A（x1，y1），B（x2，y2），
则x1+x2=-2，y1+y2=4，
分别把A，B代入椭圆方程，得：
，两式相减，得：
+
=0，
∴
+
=0，
∴k=
=
，
∴以点M（-1，2）为中点的弦所在直线方程为y-2=
(x+1)，
整理，得：2x-3y+8=0．
故选：C．
| x2 |
| 12 |
| y2 |
| 16 |
则x1+x2=-2，y1+y2=4，
分别把A，B代入椭圆方程，得：
|
| (x1+x2)(x1-x2) |
| 12 |
| (y1+y2)(y1-y2) |
| 16 |
∴
| -2(x1-x2) |
| 12 |
| 4(y1-y2) |
| 16 |
∴k=
| y1-y2 |
| x1-x2 |
| 2 |
| 3 |
∴以点M（-1，2）为中点的弦所在直线方程为y-2=
| 2 |
| 3 |
整理，得：2x-3y+8=0．
故选：C．
点评：本题考查直线方程的求法，是中档题，解题时要认真审题，注意点差法的合理运用．
练习册系列答案
相关题目
甲、乙、丙等五人站成一排，要求甲、乙均不与丙相邻，则不同的排法为（ ）
| A、72 | B、36 | C、52 | D、24 |
已知直线L的参数方程为
（t为参数 ），则直线的倾斜角为（ ）
|
A、
| ||
B、
| ||
C、
| ||
D、
|
若等差数列{an}满足：
＜-1，且其前n项和Sn有最大值．则当数列Sn＞0时，n的值为（ ）
| a11 |
| a12 |
| A、20 | B、21 | C、23 | D、22 |
等差数列{an}共有20项，其中奇数项的和为15，偶数项的和为45，则该数列的公差为（ ）
| A、-3 | B、3 | C、-2 | D、-1 |
下列命题中：
①
∥
?存在唯一的实数λ∈R，使得
=λ
②|
•
|≤|
|•|
|
③（
•
）•
=
•（
•
）
④
与
共线，
与
共线，则
与
共线
⑤若
•
=
•
且
≠0，则
=
，
其中正确命题序号是（ ）
①
| a |
| b |
| b |
| a |
②|
| a |
| b |
| a |
| b |
③（
| a |
| b |
| c |
| a |
| b |
| c |
④
| a |
| b |
| b |
| c |
| a |
| c |
⑤若
| a |
| b |
| b |
| c |
| b |
| a |
| c |
其中正确命题序号是（ ）
| A、①②⑤ | B、② | C、②⑤ | D、①④⑤ |
设f（x）=ax+a+4，若f′（1）=2，则a等于（ ）
| A、1 | B、-2 | C、2 | D、-3 |
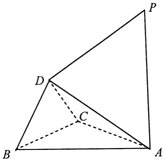已知△ABC与△DBC都是边长为2的等边三角形，且平面ABC⊥平面DBC，过点A作PA⊥平面ABC，且AP=2