题目内容
等差数列{an}共有20项，其中奇数项的和为15，偶数项的和为45，则该数列的公差为（ ）
| A、-3 | B、3 | C、-2 | D、-1 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：由题设条件知S偶-S奇=10d，从而得到数列的公差．
解答：
解：∵等差数列共有20项，其中奇数项的和为15，偶数项的和为45，
∴S偶-S奇=10d=30，
∴d=3．
故选：B．
∴S偶-S奇=10d=30，
∴d=3．
故选：B．
点评：本题考查等差数列的通项公式和前n项和公式的求法，解题时要认真审题，注意等价转化思想的合理运用．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
m∈R，复数（2m2-3m-2）+（m2-3m+2）i表示纯虚数的充要条件是（ ）
A、m=-
| ||
| B、m=2 | ||
C、m=-
| ||
| D、m=2或m=1 |
设△ABC的三个内角A，B，C所对的边分别是a，b，c，已知A=60°，a=
，c=
，则b=（ ）
| 6 |
| 2 |
A、
| ||||
B、
| ||||
C、2
| ||||
| D、3 |
在△ABC中，a=5，b=6，c=7，则
•
=（ ）
| AB |
| BC |
| A、19 | B、-19 |
| C、-14 | D、14 |
若θ为锐角，求y=3cosθ•sin2θ的最大值是（ ）
| A、3 | ||||
B、
| ||||
C、
| ||||
| D、1 |
已知椭圆
+
=1，则以点M（-1，2）为中点的弦所在直线方程为（ ）
| x2 |
| 12 |
| y2 |
| 16 |
| A、3x-8y+19=0 |
| B、3x+8y-13=0 |
| C、2x-3y+8=0 |
| D、2x+3y-4=0 |
已知tan（π-a）=2，则
=（ ）
| 1 |
| sinαcosα |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
下列函数是奇函数的是（ ）
| A、f（x）=-|x| |
| B、f（x）=2x+2-x |
| C、f（x）=lg（1+x）-lg（1-x） |
| D、f（x）=x3-1 |
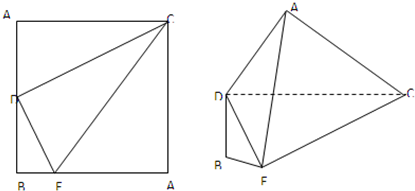如图，正方形A1BA2C的边长为4，D是A1B的中点，E是BA2上的点，将△A1DC及△A2EC分别沿DC和EC折起，使A1、A2重合于A，且平面ADC⊥平面EAC．