题目内容
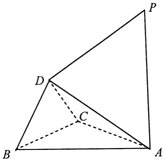 已知△ABC与△DBC都是边长为2的等边三角形,且平面ABC⊥平面DBC,过点A作PA⊥平面ABC,且AP=2
已知△ABC与△DBC都是边长为2的等边三角形,且平面ABC⊥平面DBC,过点A作PA⊥平面ABC,且AP=2| 3 |
(1)求证:PA∥平面DBC;
(2)求直线PD与平面DBC所成角的大小.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间角
分析:(1)取BC的中点O,连接DO,由已知条件推导出DO∥PA,由此能证明PA∥平面DBC.
(2)由已知条件推导出直线PD与平面ABC所成角就是直线PD与直线OA所成的角,过D作DM∥OA交PA于M,则∠PDM就是直线PD与平面DBC所成角,由此能求出结果.
(2)由已知条件推导出直线PD与平面ABC所成角就是直线PD与直线OA所成的角,过D作DM∥OA交PA于M,则∠PDM就是直线PD与平面DBC所成角,由此能求出结果.
解答:
(1)证明:取BC的中点O,连接DO,
∵△ABC与△DBC都是边长为2的等边三角形,
∴DO⊥BC,
又∵平面DBC⊥平面ABC,∴DO⊥平面ABC.
∵AP⊥平面ABC,∴DO∥PA,
又∵DO在平面DBC内,PA不包含于平面DBC,
∴PA∥平面DBC.
(2)解:∵D在平面ABC的射影是O,P在平面ABC的射影是A,
∴DP在平面ABC的射影是OA,
即直线PD与平面ABC所成角就是直线PD与直线OA所成的角,
过D作DM∥OA交PA于M,由(1)可知DO∥PA,
∴DM=OA=1,DO=MA=1,∴PM=1,
∴cos∠PDM=
=
,∴∠PDM=45°.
∴直线PD与平面DBC所成角的大小为45°.
∵△ABC与△DBC都是边长为2的等边三角形,
∴DO⊥BC,
又∵平面DBC⊥平面ABC,∴DO⊥平面ABC.
∵AP⊥平面ABC,∴DO∥PA,

又∵DO在平面DBC内,PA不包含于平面DBC,
∴PA∥平面DBC.
(2)解:∵D在平面ABC的射影是O,P在平面ABC的射影是A,
∴DP在平面ABC的射影是OA,
即直线PD与平面ABC所成角就是直线PD与直线OA所成的角,
过D作DM∥OA交PA于M,由(1)可知DO∥PA,
∴DM=OA=1,DO=MA=1,∴PM=1,
∴cos∠PDM=
| DM |
| PD |
| ||
| 2 |
∴直线PD与平面DBC所成角的大小为45°.
点评:本题考查直线与平面平行的证明,考查直线与平面所成角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数列{an}的通项公式为an=n2+1,则a5的值为( )
| A、5 | B、10 | C、17 | D、26 |
已知椭圆
+
=1,则以点M(-1,2)为中点的弦所在直线方程为( )
| x2 |
| 12 |
| y2 |
| 16 |
| A、3x-8y+19=0 |
| B、3x+8y-13=0 |
| C、2x-3y+8=0 |
| D、2x+3y-4=0 |
若将6本不同书放到5个不同盒子里,有多少种不同放法( )
A、
| ||
B、
| ||
| C、56 | ||
| D、65 |
下列函数是奇函数的是( )
| A、f(x)=-|x| |
| B、f(x)=2x+2-x |
| C、f(x)=lg(1+x)-lg(1-x) |
| D、f(x)=x3-1 |
 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6