题目内容
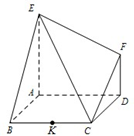 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=
如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=| 1 |
| 2 |
(Ⅰ)求多面体EABCDF的体积;
(Ⅱ)求直线EB与平面ECF所成角的正弦值;
(Ⅲ)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面ECF平行,要求保留作图痕迹,但不要求证明.
考点:棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)连接ED,多面体EABCDF的体积V=VE-PCD+VE-ABCD ,只有分别求解两个棱锥的体积即可;
(Ⅱ)以点A为原点,AB所在的直线为x轴,AD所在的直线为y轴,建立空间直角坐标系,求出平面ECF的一个法向量,利用向量的夹角公式,即可求直线EB与平面ECF所成角的正弦值;
(Ⅲ)取线段CD的中点Q;连接KQ,直线KQ即为所求.
(Ⅱ)以点A为原点,AB所在的直线为x轴,AD所在的直线为y轴,建立空间直角坐标系,求出平面ECF的一个法向量,利用向量的夹角公式,即可求直线EB与平面ECF所成角的正弦值;
(Ⅲ)取线段CD的中点Q;连接KQ,直线KQ即为所求.
解答:
 解:(Ⅰ)连接ED,
解:(Ⅰ)连接ED,
∵EA⊥底面ABCD,FD∥EA,
∴FD⊥底面ABCD,
∴FD⊥AD,FD∩AD=D,
∴AD⊥平面FDC,
VE-PCD=
AD•S△FDC=
×
×1×2×2=
,
VE-ABCD=
EA•S正方形ABCD=
×2×2×2=
,
∴多面体EABCDF的体积V=VE-PCD+VE-ABCD =
+
=
;--------------(5分)
(Ⅱ)以点A为原点,AB所在的直线为x轴,AD所在的直线为y轴,建立空间直角坐标系,如图.由已知可得A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),
∴
=(2,2,-2),
=(2,0,-2),
=(0,2,-1)------(7分)

设平面ECF的法向量为
=(x,y,z),得:
取y=1,得平面ECF的一个法向量为
=(1,1,2)------(9分)
设直线EB与平面ECF所成角为θ,
∴sinθ=|cos<
,
>|=|
|=
----(11分)
(Ⅲ)取线段CD的中点Q;连接KQ,直线KQ即为所求.---------------(12分)
如图所示…(13分)

 解:(Ⅰ)连接ED,
解:(Ⅰ)连接ED,∵EA⊥底面ABCD,FD∥EA,
∴FD⊥底面ABCD,
∴FD⊥AD,FD∩AD=D,
∴AD⊥平面FDC,
VE-PCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
VE-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
∴多面体EABCDF的体积V=VE-PCD+VE-ABCD =
| 2 |
| 3 |
| 8 |
| 3 |
| 10 |
| 3 |
(Ⅱ)以点A为原点,AB所在的直线为x轴,AD所在的直线为y轴,建立空间直角坐标系,如图.由已知可得A(0,0,0),E(0,0,2),B(2,0,0),C(2,2,0),F(0,2,1),
∴
| EC |
| EB |
| EF |

设平面ECF的法向量为
| n |
|
取y=1,得平面ECF的一个法向量为
| n |
设直线EB与平面ECF所成角为θ,
∴sinθ=|cos<
| n |
| EB |
| -2 | ||
4
|
| ||
| 6 |
(Ⅲ)取线段CD的中点Q;连接KQ,直线KQ即为所求.---------------(12分)
如图所示…(13分)

点评:本小题主要考查直线与直线,直线与平面,平面与平面位置关系等基础知识;考查空间想象能力,推理论证能力和运算求解能力.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目

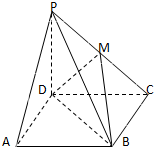 在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.
在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.
 如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,EB=
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,EB=