题目内容
2.已知函数f(x)=e|x|+x2,若实数a满足f(log2a)≤f(1),则a的取值范围是( )| A. | (0,1] | B. | [$\frac{1}{2}$,2] | C. | (0,2] | D. | [2,+∞) |
分析 可判函数f(x)为偶函数,且在[0,+∞)上是增函数,原不等式可化为|log2a|≤1,由对数函数的单调性可解.
解答 解:由题意,f(x)为偶函数,在[0,+∞)上是增函数,
∴不等式f(log2a)≤f(1)可化为|log2a|≤1,
即-1≤log2a≤1,由对数函数的单调性可得$\frac{1}{2}$≤a≤2,
故选:B.
点评 本题考查函数的单调性,涉及函数的奇偶性和对数的性质,属中档题.

练习册系列答案
相关题目
13.已知函数f(x)=e|x|,则$\int_{-2}^4{f(x)}dx$( )
| A. | e4+e2-2 | B. | e4-e2 | C. | e4-e2+2 | D. | e4-e2-2 |
14.已知函数f(x)=sinx-bcosx(其中b为实数)的图象关于直线x=-$\frac{π}{6}$对称,且?x1,x2∈R,且x1≠x2,f(x1)f(x2)≤4恒成立,则下列结论正确的是( )
| A. | 函数f(x)的图象向左平移$\frac{π}{3}$个单位得到的函数是偶函数 | |
| B. | 不等式f(x1)f(x2)≤4取到等号时|x1-x2|的最小值为2π | |
| C. | 函数f(x)的图象的一个对称中心为($\frac{2}{3}$π,0) | |
| D. | 函数f(x)在区间[$\frac{π}{6}$,π]上单调递增 |
11.设a是实数,且$\frac{2a}{1+i}$+1+i是实数,则a=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | -1 |
14.有编号为D1,D2,…,D10的10个零件,测量其直径(单位:mm),得到下面数据:
其中直径在区间(148,152]内的零件为一等品.
(1)从上述10个零件中,随机抽取2个,求这2个零件均为一等品的概率;
(2)从一等品零件中,随机抽取2个.用ξ表示这2个零件直径之差的绝对值,求随机变量ξ的分布列及数学期望.
其中直径在区间(148,152]内的零件为一等品.
| 编号 | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 |
| 直径 | 151 | 148 | 149 | 151 | 149 | 152 | 147 | 146 | 153 | 148 |
(2)从一等品零件中,随机抽取2个.用ξ表示这2个零件直径之差的绝对值,求随机变量ξ的分布列及数学期望.
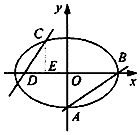 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,直线AB分别交椭圆下顶点A(0,-1)和右顶点B.
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$(a>b>0)的离心率$e=\frac{{\sqrt{6}}}{3}$,直线AB分别交椭圆下顶点A(0,-1)和右顶点B. 