题目内容

5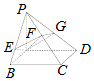．如图，PA⊥平面ABCD，底面ABCD为矩形，AE⊥PB于E，AF⊥PC于F
（1）求证：PC⊥面AEF；
（2）设平面AEF交PD于G，求证：AG⊥PD．

分析 （1）由ABCD为矩形，得BC⊥AB有PA⊥平面ABCD可知BC⊥平面PAB，从而AE⊥BC，可证AE⊥PC，由AF⊥PC，AE∩AF=A，从而证明PC⊥面AEF；
（2）由ABCD为矩形，可证CD⊥平面PAD，得CD⊥AG，可知PC⊥AG，从而AG⊥平面PCD，可证AG⊥PD．

解答 解：（1）∵ABCD为矩形
∴BC⊥AB
∵PA⊥平面ABCD
∴BC⊥PA
∴BC⊥平面PAB
∴AE⊥BC
又AE⊥PB
∴AE⊥平面PBC
∴AE⊥PC
又AF⊥PC，AE∩AF=A，
∴PC⊥平面AEF；
（2）∵ABCD为矩形
∴CD⊥AD
∵PA⊥平面ABCD
∴CD⊥PA
∴CD⊥平面PAD
∴CD⊥AG
∵PC⊥平面AEF
∴PC⊥AG
∴AG⊥平面PCD
∴AG⊥PD

点评 本题主要考查了直线与平面垂直的性质，直线与平面垂直的判定，属于基本知识的考查．

练习册系列答案
相关题目
15．设实数a，b满足a+2b=9．
（1）若|9-2b|+|a+1|＜3，求a的取值范围；
（2）若a，b＞0，且z=ab2，求z的最大值．
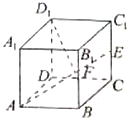
16．在正方体ABCD-A1B1C1D1中，E，F分别为CC1和BB1的中点，则异面直线AE与D1F所成角的余弦值为（　　）
A．0B．$\frac{{\sqrt{3}}}{12}$C．$\frac{{\sqrt{3}}}{3}$D．$\frac{1}{9}$
13．函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{{3}^{x}，x≤0}\end{array}\right.$，则f（f（$\frac{1}{4}$））=（　　）
A．$\frac{1}{9}$B．$\frac{1}{6}$C．$\frac{1}{3}$D．1
20．已知函数f（x）=a-$\frac{2}{{2}^{x}+1}$（a∈R）．
（1）判断函数f（x）的单调性，并用定义法证明；
（2）若a=1，求f（-5）+f（-3）+f（-1）+f（1）+f（3）+f（5）的值．
10．某班对一次实验成绩进行分析，利用随机数表法抽取样本时，先将50个同学按01，02，03…50进行编号，然后从随机数表第9行第11列的数开始向右读，则选出的第7个个体是（　　）
（注：表为随机数表的第8行和第9行）
A．02B．13C．42D．44
17．已知$cos（\frac{π}{6}-α）=\frac{{\sqrt{3}}}{3}$．
（1）求$cos（\frac{5π}{6}+α）$的值；
（2）求$sin（\frac{2π}{3}-α）$的值．
14．若函数y=f（x）的图象上存在两个点A，B，且关于原点对称，则称点对[A，B]为函数y=f（x）的“友情点对”，点对[A，B]与[B，A]可看作同一个“友情点对”，若函数$f（x）=\left\{\begin{array}{l}2，x＜0\\-{x^3}+6{x^2}-9x+a，x≥0\end{array}\right.$恰好由两个“友情点对”，则实数a的值为（　　）
A．-2B．2C．1D．0
15．直线mx+$\frac{n}{2}$y-1=0在y轴上的截距是-1，且它的倾斜角是直线$\sqrt{3}x-y-3\sqrt{3}$=0的倾斜角的2倍，则（　　）
A．m=-$\sqrt{3}$，n=-2B．m=$\sqrt{3}$，n=2C．m=$\sqrt{3}$，n=-2D．m=-$\sqrt{3}$，n=2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网