题目内容
13．函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{{3}^{x}，x≤0}\end{array}\right.$，则f（f（$\frac{1}{4}$））=（ ）| A． | $\frac{1}{9}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{3}$ | D． | 1 |
分析 由分段函数解析式，先求f（$\frac{1}{4}$），再由f（f（$\frac{1}{4}$））的值．
解答 解：函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x，x＞0}\\{{3}^{x}，x≤0}\end{array}\right.$，
可得f（$\frac{1}{4}$）=log2$\frac{1}{4}$=-2，
则f（f（$\frac{1}{4}$））=f（-2）=3-2=$\frac{1}{9}$．
故选：A．
点评 本题考查分段函数值的求法，注意各段的解析式的运用，考查运算能力，属于基础题．
练习册系列答案
相关题目
3．已知O为△ABC内一点，且$\overrightarrow{AO}=\frac{1}{2}（\overrightarrow{OB}+\overrightarrow{OC}）$，$\overrightarrow{AD}=t\overrightarrow{AC}$，若B，O，D三点共线，则t的值为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
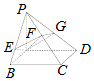如图，PA⊥平面ABCD，底面ABCD为矩形，AE⊥PB于E，AF⊥PC于F
在ABC-A1B1C1中，所有棱长均相等，且∠ABB1=60°，D为AC的中点，求证：