题目内容
20.已知函数f(x)=a-$\frac{2}{{2}^{x}+1}$(a∈R).(1)判断函数f(x)的单调性,并用定义法证明;
(2)若a=1,求f(-5)+f(-3)+f(-1)+f(1)+f(3)+f(5)的值.
分析 (1)先判断出函数的单调性,再利用函数的单调性的定义进行证明即可;
(2)求出f(-x)+f(x)=0,求出函数值即可.
解答 (1)证明:f(x)在(-∞,+∞)上是增函数,证明如下:
设任意的x1,x2∈(-∞,+∞)且x1<x2
则f(x1)-f(x2)=a-$\frac{2}{{2}^{{x}_{1}}+1}$-(a-$\frac{2}{{2}^{{x}_{2}}+1}$)=$\frac{2{(2}^{{x}_{1}}{-2}^{{x}_{2}})}{{(2}^{{x}_{1}}+1){(2}^{{x}_{2}}+1)}$,
∵x1<x2,∴2x1-2x2<0,则 $\frac{2{(2}^{{x}_{1}}{-2}^{{x}_{2}})}{{(2}^{{x}_{1}}+1){(2}^{{x}_{2}}+1)}$<0,
即f(x1)-f(x2)<0,
∴f(x1)<f(x2),
∴f(x)在(-∞,+∞)上是增函数;
(2)a=1时,f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$,
而f(x)+f(-x)=0,
故f(-5)+f(-3)+f(-1)+f(1)+f(3)+f(5)=0.
点评 本题主要考查函数的单调性的证明方法:定义法,以及利用函数单调性求函数值问题,属于中档题.

练习册系列答案
相关题目
11.若六棱柱ABCDEF-A1B1C1D1E1F1的底面是边长为1的正六边形,侧棱AA1⊥底面ABCDEF,且$A{A_1}=\sqrt{6}$,则异面直线EF与BD1所成的角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
15.要得到函数y=sin2x的图象,只要将函数y=sin(2x+$\frac{π}{3}$)的图象( )
| A. | 向左平移$\frac{π}{6}$单位即可 | B. | 向右平移$\frac{π}{6}$单位即可 | ||
| C. | 向右平移$\frac{π}{3}$单位即可 | D. | 向左平移$\frac{π}{3}$单位即可 |
12.已知实数a,b满足2a=3,3b=2,则函数f(x)=ax+x-b的零点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
9.$\int_{\frac{π}{2}}^π{sinx}dx$的值为( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{1}{2}$ | D. | 1 |


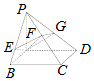 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F
如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F