题目内容
17.已知$cos(\frac{π}{6}-α)=\frac{{\sqrt{3}}}{3}$.(1)求$cos(\frac{5π}{6}+α)$的值;
(2)求$sin(\frac{2π}{3}-α)$的值.
分析 (1)根据$(\frac{5π}{6}+α)+(\frac{π}{6}-α)=π$,构造同角化简即可.
(2)根据$\frac{2π}{3}-α=\frac{π}{2}+(\frac{π}{6}-α)$,构造同角化简即可.
解答 解:由题意$cos(\frac{π}{6}-α)=\frac{{\sqrt{3}}}{3}$.
(1)∵$(\frac{5π}{6}+α)+(\frac{π}{6}-α)=π$,
∴$cos(\frac{5π}{6}+α)=cos[π-(\frac{π}{6}-α)]=-cos(\frac{π}{6}-α)=-\frac{{\sqrt{3}}}{3}$.
(2)∵$\frac{2π}{3}-α=\frac{π}{2}+(\frac{π}{6}-α)$,
∴$sin(\frac{2π}{3}-α)=sin[\frac{π}{2}+(\frac{π}{6}-α)]=cos(\frac{π}{6}-α)=\frac{{\sqrt{3}}}{3}$.
点评 本题考查了诱导公式的运用,角度的构造思想.属于基础题.

练习册系列答案
相关题目
7.已知a>0且a≠1,如图所示的程序框图的输出值y∈[4,+∞),则实数a的取值范围是( )
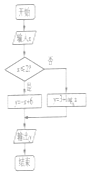

| A. | (1,2] | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | [2,+∞) |
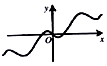
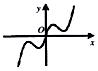
12.已知实数a,b满足2a=3,3b=2,则函数f(x)=ax+x-b的零点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
9.$\int_{\frac{π}{2}}^π{sinx}dx$的值为( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{1}{2}$ | D. | 1 |


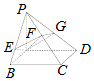 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F
如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F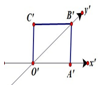 如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的周长是16cm,面积是$8\sqrt{2}c{m^2}$.
如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的周长是16cm,面积是$8\sqrt{2}c{m^2}$. 如图,在△ABC中,边BC上的高所在的直线方程为x-3y+2=0,∠BAC的平分线所在的直线方程为y=0,若点B的坐标为(1,3).
如图,在△ABC中,边BC上的高所在的直线方程为x-3y+2=0,∠BAC的平分线所在的直线方程为y=0,若点B的坐标为(1,3).