题目内容
16.在正方体ABCD-A1B1C1D1中,E,F分别为CC1和BB1的中点,则异面直线AE与D1F所成角的余弦值为( )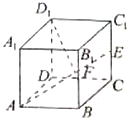
| A. | 0 | B. | $\frac{{\sqrt{3}}}{12}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{1}{9}$ |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线AE与D1F所成角的余弦值.
解答  解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,
则A(2,0,0),E(0,2,1),D1(0,0,2),F(2,2,1),
$\overrightarrow{AE}$=(-2,2,1),$\overrightarrow{{D}_{1}F}$=(2,2,-1),
设直线AE与D1F所成角为θ,
则cosθ=|$\frac{-4+4-1}{\sqrt{4+4+1}•\sqrt{4+4+1}}$|=$\frac{1}{9}$.
∴直线AE与D1F所成角的余弦值为$\frac{1}{9}$.
故选D.
点评 本题考查两异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
6.集合A={x|x≤a},B={1,2},A∩B=∅,则a的取值范围为( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (2,+∞) | D. | (-∞,2) |
7.已知a>0且a≠1,如图所示的程序框图的输出值y∈[4,+∞),则实数a的取值范围是( )
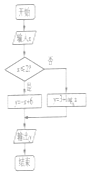

| A. | (1,2] | B. | ($\frac{1}{2}$,1) | C. | (1,2) | D. | [2,+∞) |
11.若六棱柱ABCDEF-A1B1C1D1E1F1的底面是边长为1的正六边形,侧棱AA1⊥底面ABCDEF,且$A{A_1}=\sqrt{6}$,则异面直线EF与BD1所成的角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |


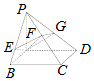 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F
如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于E,AF⊥PC于F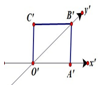 如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的周长是16cm,面积是$8\sqrt{2}c{m^2}$.
如图所示正方形O'A'B'C'的边长为2cm,它是一个水平放置的一个平面图形的直观图,则原图形的周长是16cm,面积是$8\sqrt{2}c{m^2}$.