题目内容
以下命题正确的个数为 .
①因为数列可以看出函数,所以每个数列均有通项公式;
②引入向量坐标的理论依据是平面向量的分解定理;
③由于矩阵与行列式都用行与列的形式呈现数据,因此两者本质上没区别;
④确定一条直线的基本要素是点和方向,两者缺一不可;
⑤过点P(x0,y0)且与向量
=(u,v)平行的直线方程是
=
.
①因为数列可以看出函数,所以每个数列均有通项公式;
②引入向量坐标的理论依据是平面向量的分解定理;
③由于矩阵与行列式都用行与列的形式呈现数据,因此两者本质上没区别;
④确定一条直线的基本要素是点和方向,两者缺一不可;
⑤过点P(x0,y0)且与向量
| d |
| x-x0 |
| u |
| y-y0 |
| v |
考点:命题的真假判断与应用
专题:简易逻辑
分析:根据数列不一定有通项公式,可判断①;根据引入向量坐标的理论依据是平面向量的基本(分解)定理,可判断②;根据矩阵与行列式在行列数关系,相等的定义等方面均不相同,可判断③;根据两点也可以确定直线,可判断④;根据点向式方式的前提条件是u≠0,v≠0,可判断⑤.
解答:
解:对于①,每个数列不一定有通项公式,故错误;
对于②,引入向量坐标的理论依据是平面向量的基本(分解)定理,故正确;
对于③,矩阵与行列式在行列数关系,相等的定义等方面均不相同,故错误;
对于④,两点也可以确定直线,故错误;
对于⑤,过点P(x0,y0)且与向量
=(u,v)平行的直线方程是
=
的前提是u≠0,v≠0,故错误;
故答案为:1
对于②,引入向量坐标的理论依据是平面向量的基本(分解)定理,故正确;
对于③,矩阵与行列式在行列数关系,相等的定义等方面均不相同,故错误;
对于④,两点也可以确定直线,故错误;
对于⑤,过点P(x0,y0)且与向量
| d |
| x-x0 |
| u |
| y-y0 |
| v |
故答案为:1
点评:本题考查的知识点是命题的真假判断与应用,在判断时要注意对所涉及的基本概念的深入理解,难度不大,属于基础题.

练习册系列答案
相关题目
 如图所示,已知A,B均为集合U={1,2,5,7,11}的子集,且A∩B={2},(∁UB)∩A={11},则集合A等于
如图所示,已知A,B均为集合U={1,2,5,7,11}的子集,且A∩B={2},(∁UB)∩A={11},则集合A等于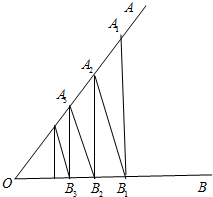 如图,相交于点O的两条直线OA,OB,在OA上取一点A,作A1B1⊥OB,作B1A2⊥OA,作A2B2⊥OB…一直无限地作下去,若已知A1B1=7,B1A2=6,则所有垂线长度的和等于
如图,相交于点O的两条直线OA,OB,在OA上取一点A,作A1B1⊥OB,作B1A2⊥OA,作A2B2⊥OB…一直无限地作下去,若已知A1B1=7,B1A2=6,则所有垂线长度的和等于