题目内容
设函数f（x）=
x3+ax2-9x-1（a＞0），直线l是曲线y=f（x）的一条切线，当l斜率最小时，直线l与直线10x+y=6平行．
（1）求a的值；
（2）求f（x）在x=3处的切线方程．
| 1 |
| 3 |
（1）求a的值；
（2）求f（x）在x=3处的切线方程．
考点：利用导数研究曲线上某点切线方程,直线的一般式方程与直线的平行关系
专题：导数的综合应用
分析：（1）求出函数的导数，利用切线的斜率的最小值，以及直线l与直线10x+y=6平行．即可求a的值；
（2）利用（1）得到函数的解析式，求出函数的对数，求出切点坐标，斜率，利用点斜式即可求解f（x）在x=3处的切线方程．
（2）利用（1）得到函数的解析式，求出函数的对数，求出切点坐标，斜率，利用点斜式即可求解f（x）在x=3处的切线方程．
解答：
解：（1）函数f（x）=
x3+ax2-9x-1，可得f′（x）=x2+2ax-9=（x+a）2-9-a2
∴斜率的最小值为-9-a2，直线l与直线10x+y=6平行．
∴-9-a2=-10．
得：a=1．
（2）则f(x)=
x3+x2-9x-1，f′（x）=x2+2x-9
则f（3）=-10，f′（3）=6，
切点坐标为：（3，-10），
切线为：y+10=6（x-3）．
即：y=6x-28．
| 1 |
| 3 |
∴斜率的最小值为-9-a2，直线l与直线10x+y=6平行．
∴-9-a2=-10．
得：a=1．
（2）则f(x)=
| 1 |
| 3 |
则f（3）=-10，f′（3）=6，
切点坐标为：（3，-10），
切线为：y+10=6（x-3）．
即：y=6x-28．
点评：本题考查函数的导数的应用，切线的斜率以及切线方程的求法，考查计算能力．
练习册系列答案
阅读快车系列答案
相关题目
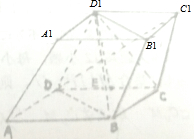如图，在平行六面体ABCD-A1B1C1D1中，底面是边长为a的正方形，D1是底面ABCD上的射影E恰好是CD的中点，BD1⊥DC1．
已知抛物线y2=4x内一定点E（m，0），（m＞0），过点E作斜率分别为k1，k2的两条直线，交抛物线于A、B和C、D，且M，N分别是线段AB、CD的中点．
如图所示，圆O的直径为BD，过圆上一点A作圆O的切线AE，过点D作DE⊥AE于点E，延长ED与圆O交于点C．