题目内容
从一批有10件合格品与3件次品的产品中,一件一件地抽取产品,设各件产品被抽取到的可能性相同,在下列两种情况下,分别求出直到取到合格品为止所需抽取的次数X的分布列.
(1)每次取出的产品都不放回该批产品中;
(2)每次取出的产品都立即放回该批产品中.
(1)每次取出的产品都不放回该批产品中;
(2)每次取出的产品都立即放回该批产品中.
考点:离散型随机变量及其分布列
专题:概率与统计
分析:(1)若每次取出的产品都不放回该批产品中,则X的取值可能为:1,2,3,4,依次计算出X=1,2,3,4时的概率,可得抽取次数X的分布列.
(2)若每次取出的产品都放回该批产品中,则X的取值可能为:1,2,3,4,…,依次计算出X=1,2,3,…,n,…时的概率,可得抽取次数X的分布列.
(2)若每次取出的产品都放回该批产品中,则X的取值可能为:1,2,3,4,…,依次计算出X=1,2,3,…,n,…时的概率,可得抽取次数X的分布列.
解答:
解:(1)若每次取出的产品都不放回该批产品中,
则X的取值可能为:1,2,3,4,
P(X=1)=
,
P(X=2)=
•
=
,
P(X=3)=
•
•
=
,
P(X=4)=
•
•
•
=
,
∴X的分布如下:
(2)若每次取出的产品都立即放回该批产品中.
则X的取值可能为:1,2,3,4,…
P(X=1)=
,
P(X=2)=
•
=
,
P(X=3)=
•
•
=
,
…
P(X=n)=
•
•…•
•
=
,
∴X的分布如下:
则X的取值可能为:1,2,3,4,
P(X=1)=
| 10 |
| 13 |
P(X=2)=
| 3 |
| 13 |
| 10 |
| 12 |
| 5 |
| 26 |
P(X=3)=
| 3 |
| 13 |
| 2 |
| 12 |
| 10 |
| 11 |
| 5 |
| 143 |
P(X=4)=
| 3 |
| 13 |
| 2 |
| 12 |
| 1 |
| 11 |
| 10 |
| 10 |
| 1 |
| 286 |
∴X的分布如下:
| X | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
则X的取值可能为:1,2,3,4,…
P(X=1)=
| 10 |
| 13 |
P(X=2)=
| 3 |
| 13 |
| 10 |
| 13 |
| 3×10 |
| 132 |
P(X=3)=
| 3 |
| 13 |
| 3 |
| 13 |
| 10 |
| 13 |
| 32×10 |
| 133 |
…
P(X=n)=
| 3 |
| 13 |
| 3 |
| 13 |
| 3 |
| 13 |
| 10 |
| 13 |
| 3n-1×10 |
| 13n |
∴X的分布如下:
| X | 1 | 2 | 3 | … | n | … | ||||||||
| P |
|
|
| … |
| … |
点评:本题考查离散型随机变量的分布列,属中档题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
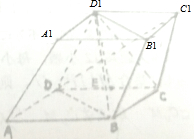 如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为a的正方形,D1是底面ABCD上的射影E恰好是CD的中点,BD1⊥DC1.
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为a的正方形,D1是底面ABCD上的射影E恰好是CD的中点,BD1⊥DC1. 已知抛物线y2=4x内一定点E(m,0),(m>0),过点E作斜率分别为k1,k2的两条直线,交抛物线于A、B和C、D,且M,N分别是线段AB、CD的中点.
已知抛物线y2=4x内一定点E(m,0),(m>0),过点E作斜率分别为k1,k2的两条直线,交抛物线于A、B和C、D,且M,N分别是线段AB、CD的中点.