题目内容
ABCD是边长为3的正方形，ABEF是矩形，面ABCD垂直于面ABEF，G为EC的中点，求证AC∥面BFG．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：由题意，画出图形，利用线面平行的判定定理，只要在平面BFG内找出一条直线与AC平行即可．
解答：
证明：如图，
连接AE，交BF与O，则O是AE的中点，又G是EC的中点，
所以AC∥OG，
又AC?平面BFG，OG?平面BFG，
所以AC∥面BFG．
连接AE，交BF与O，则O是AE的中点，又G是EC的中点，
所以AC∥OG，
又AC?平面BFG，OG?平面BFG，
所以AC∥面BFG．
点评：本题考查了线面平行的判定定理的运用；关键是在平面BFG内找出与AC平行的直线．
练习册系列答案
相关题目
若关于x的方程ax3-3x2+1=0正实数解有且仅有一个，则实数a的取值范围是（ ）
| A、{a|a≤0} |
| B、{a|a≤0或a=2} |
| C、{a|a≥0} |
| D、{a|a≥0或a=-2} |
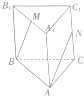已知正三棱柱ABC-A1B1C1的底面边长是2，侧棱长为4，M、N分别是A1B1，CC1中点，则AN与BM所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若存在x使2•（x-a）＞1成立．则a的取值范围是（ ）
| A、（-∞．+∞） |
| B、（-2，+∞） |
| C、（0．+∞） |
| D、（-1，+∞） |