题目内容
等差数列{an}的前n项和Sn
(1)求数列{
}是等差数列
(2)若a1=1,且对任意正整数n,k(n>k),都有
+
=2
成立,求数列{an}的通项公式.
(3)记bn=a(a>0),求证:
≤
.
(1)求数列{
| Sn |
| n |
(2)若a1=1,且对任意正整数n,k(n>k),都有
| Sn+k |
| Sn-k |
| Sn |
(3)记bn=a(a>0),求证:
| b1+b2+…+bn |
| n |
| b1+bn |
| 2 |
考点:数列递推式,等差关系的确定,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由等差数列的前n项和公式求出Sn,再化简
和
-
,利用等差数列的定义即可证明;
(2)由题意令k=1代入
+
=2
,利用等差中项的性质可得数列{
}是等差数列,设其公差为t,利用等差数列的通项公式求出Sn,再由当n≥2时an=Sn-Sn-1、等差数列{an}的定义求出公差t,代入当n≥2时an=Sn-Sn-1化简的式子即可;
(3)把bn=a代入不等式的左边和右边化简即可.
| Sn |
| n |
| Sn |
| n |
| Sn-1 |
| n-1 |
(2)由题意令k=1代入
| Sn+k |
| Sn-k |
| Sn |
| Sn |
(3)把bn=a代入不等式的左边和右边化简即可.
解答:
证明:(1)设等差数列{an}的公差为d,则Sn=na1+
×d,
则
=a1+
×d,
所以
-
=(a1+
×d)-(a1+
×d)=
,
则数列{
}是以
为公差的等差数列;
解:(2)因为对任意正整数n,k(n>k),都有
+
=2
成立,
所以
+
=2
,
即数列{
}是等差数列,设其公差为t,且a1=1,
则
=
+(n-1)t=1+(n-1)t,即Sn=[1+(n-1)t]2,
所以当n≥2时,an=Sn-Sn-1=[1+(n-1)t]2-[1+(n-2)t]2=2t2n-3t2+2t,
又在等差数列{an}中,a2-a1=a3-a2,
即(4t2-3t2+2t)-1=(6t2-3t2+2t)-(4t2-3t2+2t),解得t=1,
代入an=2t2n-3t2+2t,化简得an=2n-1;
证明:(3)由题意得,bn=a(a>0),
所以
=
=a,
=
=a,
则
≤
成立.
| n(n-1) |
| 2 |
则
| Sn |
| n |
| n-1 |
| 2 |
所以
| Sn |
| n |
| Sn-1 |
| n-1 |
| n-1 |
| 2 |
| n-2 |
| 2 |
| d |
| 2 |
则数列{
| Sn |
| n |
| d |
| 2 |
解:(2)因为对任意正整数n,k(n>k),都有
| Sn+k |
| Sn-k |
| Sn |
所以
| Sn+1 |
| Sn-1 |
| Sn |
即数列{
| Sn |
则
| Sn |
| S1 |
所以当n≥2时,an=Sn-Sn-1=[1+(n-1)t]2-[1+(n-2)t]2=2t2n-3t2+2t,
又在等差数列{an}中,a2-a1=a3-a2,
即(4t2-3t2+2t)-1=(6t2-3t2+2t)-(4t2-3t2+2t),解得t=1,
代入an=2t2n-3t2+2t,化简得an=2n-1;
证明:(3)由题意得,bn=a(a>0),
所以
| b1+b2+…+bn |
| n |
| na |
| n |
| b1+bn |
| 2 |
| 2a |
| 2 |
则
| b1+b2+…+bn |
| n |
| b1+bn |
| 2 |
点评:本题考查等差数列的定义、通项公式以及前n项和公式,以及数列的前n项和与通项的关系式的应用,考查化简计算能力,属于中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
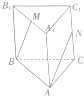 已知正三棱柱ABC-A1B1C1的底面边长是2,侧棱长为4,M、N分别是A1B1,CC1中点,则AN与BM所成角的余弦值为( )
已知正三棱柱ABC-A1B1C1的底面边长是2,侧棱长为4,M、N分别是A1B1,CC1中点,则AN与BM所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
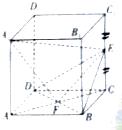 如图,正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC与BD的交点.
如图,正方体ABCD-A1B1C1D1中,E是CC1的中点,F是AC与BD的交点. 给出下列四个结论:
给出下列四个结论:
