题目内容
求下列函数的最大值和最小值,并写出取得最大值和最小值时的自变量x的值.
(1)y=2sinx,x∈[-
,π];
(2)y=3cosx,x∈(-
,
];
(3)y=-
sinx,x∈(-
,
).
(1)y=2sinx,x∈[-
| π |
| 6 |
(2)y=3cosx,x∈(-
| π |
| 6 |
| 4π |
| 3 |
(3)y=-
| 1 |
| 2 |
| 5π |
| 6 |
| 3π |
| 4 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:分别求出角的范围,结合三角函数的图象即可得到结论.
解答:
解:(1)∵x∈[-
,π],∴当x=
时,函数取得最大值2,
∴当x=-
时,函数取得最小值2sin(-
)=-
×2=-1.
(2)∵x∈(-
,
],
∴当x=0时,函数取得最大值3,
∴当x=
时,函数取得最小值3cos
=-
×3=-
;
(3)∵x∈(-
,
).
∴当x=-
时,函数取得最大值
,
当x=
时,函数取得最小值-
,
| π |
| 6 |
| π |
| 2 |
∴当x=-
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
(2)∵x∈(-
| π |
| 6 |
| 4π |
| 3 |
∴当x=0时,函数取得最大值3,
∴当x=
| 4π |
| 3 |
| 4π |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
(3)∵x∈(-
| 5π |
| 6 |
| 3π |
| 4 |
∴当x=-
| π |
| 2 |
| 1 |
| 2 |
当x=
| π |
| 2 |
| 1 |
| 2 |
点评:本题主要考查三角函数的最值,根据正弦函数的单调性结合角的取值范围是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若tan(7π+α)=a,则
的值为( )
| sin(α-3π)+cos(π-α) |
| sin(-α)-cos(π+α) |
A、
| ||
B、
| ||
| C、-1 | ||
| D、1 |
函数f(x)=lnx+2x-8的零点所在区间是( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
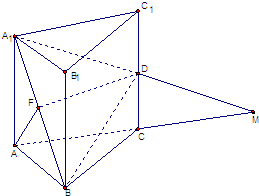 已知:正三棱柱A1B1C1-ABC中,AA1=AB=a,D为CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M.
已知:正三棱柱A1B1C1-ABC中,AA1=AB=a,D为CC1的中点,F是A1B的中点,A1D与AC的延长线交于点M. 已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点
已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点 如图所示的几何体中,四边形ABCD与BDEF是边长均为a的菱形,FA=FC
如图所示的几何体中,四边形ABCD与BDEF是边长均为a的菱形,FA=FC