题目内容
 已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点
已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点(1)求证:EFGH是平行四边形
(2)若BD=2
| 3 |
考点:异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)由已知得EH∥BD,FG∥BD,从而EH∥FG,EH=FG,由此能证明四边形EFGH是平行四边形.
(2)由条件可知AC与BD所成的角为∠EHG,连接EG,由勾股定理得AC与BD所成的角为90°.
②EG、BD所成的角为∠GEH,在Rt△EHG中,sin∠GEH=
=
,由此能求出EG、BD所成的角为30°.
(2)由条件可知AC与BD所成的角为∠EHG,连接EG,由勾股定理得AC与BD所成的角为90°.
②EG、BD所成的角为∠GEH,在Rt△EHG中,sin∠GEH=
| HG |
| EG |
| 1 |
| 2 |
解答:
(本题14分)
(1)证明:在△ABD中,∵E、H分别是AB,AD的中点,
∴EH∥BD,EH=
BD,
同理,FG∥BD,FG=
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
(2)解:①由条件可知AC与BD所成的角为∠EHG,
连接EG,∵EH=
BD=
,HG=
AC=1,EG=2
在△EGH中,EH2+GH2=4=EG2,
∴EH⊥HG,即AC与BD所成的角为90°.
②EG、BD所成的角为∠GEH,在Rt△EHG中,
Sin∠GEH=
=
,
∴∠GEH=30°,
∴EG、BD所成的角为30°.
(1)证明:在△ABD中,∵E、H分别是AB,AD的中点,

∴EH∥BD,EH=
| 1 |
| 2 |
同理,FG∥BD,FG=
| 1 |
| 2 |
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
(2)解:①由条件可知AC与BD所成的角为∠EHG,
连接EG,∵EH=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
在△EGH中,EH2+GH2=4=EG2,
∴EH⊥HG,即AC与BD所成的角为90°.
②EG、BD所成的角为∠GEH,在Rt△EHG中,
Sin∠GEH=
| HG |
| EG |
| 1 |
| 2 |
∴∠GEH=30°,
∴EG、BD所成的角为30°.
点评:本题考查四边形是平行四边形的证明,考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
方程x2+y2+2x-4y-6=0表示的圆形是( )
A、以(1,-2)为圆心,
| ||
B、以(1,2)为圆心,
| ||
C、以(-1,-2)为圆心,
| ||
D、以(-1,2)为圆心,
|
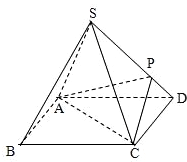 在正四棱锥S-ABCD中,底面边长为a,侧棱长为
在正四棱锥S-ABCD中,底面边长为a,侧棱长为| 2 |
(1)当正面体ACPS的体积为
| ||
| 18 |
| SP |
| PD |
(2)在(1)的条件下,若E是SC的中点,求证:BE∥平面APC.
正方体ABCD-A1B1C1D1中,AB1与C1D1所成的角( )
| A、30° | B、45° |
| C、60° | D、90° |
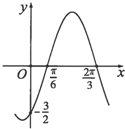 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<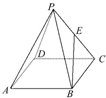 如图所示,正四棱锥P-ABCD的底面积为3,体积为
如图所示,正四棱锥P-ABCD的底面积为3,体积为