题目内容
曲线C1的参数方程为
(θ为参数),将曲线C1上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的
倍,得到曲线C2.以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(cosθ-2sinθ)=6.
(1)求曲线C2和直线l的普通方程;
(2)P为曲线C2上任意一点,求点P到直线l的距离的最值.
|
| 3 |
(1)求曲线C2和直线l的普通方程;
(2)P为曲线C2上任意一点,求点P到直线l的距离的最值.
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(Ⅰ)把C2的参数方程利用同角三角函数的基本关系消去参数,化为直角坐标方程;把直线l的极坐标方程根据x=ρcosθ、y=ρsinθ化为直角坐标方程.
(Ⅱ)设点P(2cosθ,
sinθ),由点到直线的距离公式得点P到直线l的距离为d=
[6+4sin(θ-
)],根据正弦函数的值域求得点P到直线l的距离的最大值和最小值.
(Ⅱ)设点P(2cosθ,
| 3 |
| ||
| 5 |
| π |
| 6 |
解答:
解:(Ⅰ)由题意可得C2的参数方程为
(θ为参数),即C2:
+
=1,
直线l:ρ(cosθ-2sinθ)=6,化为直角坐标方程为 x-2y-6=0.
(Ⅱ)设点P(2cosθ,
sinθ),由点到直线的距离公式得点P到直线l的距离为
d=
=
=
=
[6+4sin(θ-
)].
∴
≤d≤2
,故点P到直线l的距离的最大值为2
,最小值为
.
|
| x2 |
| 4 |
| y2 |
| 3 |
直线l:ρ(cosθ-2sinθ)=6,化为直角坐标方程为 x-2y-6=0.
(Ⅱ)设点P(2cosθ,
| 3 |
d=
|2cosθ-2
| ||
|
|6+4(
| ||||||
|
|6+4sin(θ-
| ||
|
| ||
| 5 |
| π |
| 6 |
∴
2
| ||
| 5 |
| 5 |
| 5 |
2
| ||
| 5 |
点评:题主要考查把参数方程、极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,正弦函数的值域,属于基础题.

练习册系列答案
相关题目
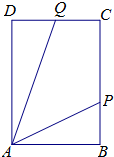 如图,ABCD是长方形海域,其中AB=10海里,AD=10
如图,ABCD是长方形海域,其中AB=10海里,AD=10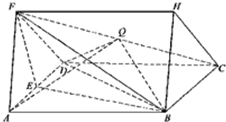 如图,三棱柱ADF-BCH中,侧面ABCD是菱形,FA=FD,∠BAD=60°,E是AD的中点,点Q在线段FC上.
如图,三棱柱ADF-BCH中,侧面ABCD是菱形,FA=FD,∠BAD=60°,E是AD的中点,点Q在线段FC上. 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=