题目内容
已知二次函数f(x)=x2-2ax+b2(a,b∈R),若a是从区间[-2,2]中随机抽取的一个数,b是从区间[-3,3]中随机抽取的一个数,求方程f(x)=0没有实数根的概率.
考点:几何概型
专题:概率与统计
分析:由方程f(x)=0没有实数根,可求出a,b满足的条件,然后求出实验的全部结果构成的区域的面积,再求出方程f(x)=0没有实数根的区域的面积,即可求得方程f(x)=0没有实数解的概率.
解答:
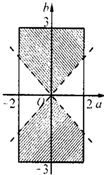 解:由方程f(x)=0没有实数根,
解:由方程f(x)=0没有实数根,
得:4a2-4b2<0,∴(a-b)(a+b)<0,
即:
或者
,
又因为-2≤a≤2,-3≤b≤3,
作出平面区域图如图所示,
可知方程f(x)=0没有实数根的概率为:P=
=
,
故方程f(x)=0没有实数根的概率为
.
 解:由方程f(x)=0没有实数根,
解:由方程f(x)=0没有实数根,得:4a2-4b2<0,∴(a-b)(a+b)<0,
即:
|
|
又因为-2≤a≤2,-3≤b≤3,
作出平面区域图如图所示,
可知方程f(x)=0没有实数根的概率为:P=
4×6-2×
| ||
| 4×6 |
| 2 |
| 3 |
故方程f(x)=0没有实数根的概率为
| 2 |
| 3 |
点评:本题主要考查几何概型,二次函数的性质的应用,体现了转化的数学思想,同时考查了作图的能力和运算求解的能力,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
设函数f(x)=
,则f(log23)=( )
|
A、
| ||
B、
| ||
C、
| ||
D、-
|
已知全集U=R,集合A={x|1<x<4},B={x|x≥2},则A∩∁UB=( )
| A、{x|1<x≤2} |
| B、{x|2<x<4} |
| C、{x|1<x<2} |
| D、{x|x<2} |
 从一个棱长为3的正方体中切去一些部分,得到一个几何体,其三视图如图,则该几何体的体积为( )
从一个棱长为3的正方体中切去一些部分,得到一个几何体,其三视图如图,则该几何体的体积为( )| A、3 | B、7 | C、9 | D、18 |