题目内容
双曲线
-
=1渐近线方程为 .
| x2 |
| 4 |
| y2 |
| 12 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:在双曲线的标准方程中,把1换成0,即得此双曲线的渐近线方程.
解答:
解:在双曲线的标准方程中,把1换成0,
即得
-
=1的渐近线方程为
-
=0,化简可得y=±
x.
故答案为:y=±
x.
即得
| x2 |
| 4 |
| y2 |
| 12 |
| x2 |
| 4 |
| y2 |
| 12 |
| 3 |
故答案为:y=±
| 3 |
点评:本题以双曲线为载体,考查双曲线的简单性质,解题的关键是正确运用双曲线的标准方程.

练习册系列答案
相关题目
经过双曲线x2-y2=8的右焦点且斜率为2的直线被双曲线截得的线段的长是( )
A、
| ||||
B、7
| ||||
C、2
| ||||
D、
|
函数y=loga(3x-1)(a>0,a≠1)的图象过定点( )
A、(
| ||
| B、(-1,0) | ||
C、(
| ||
| D、(0,-1) |
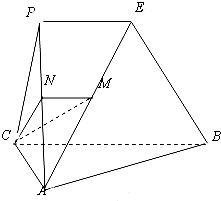 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥BC,过BC作平面交AP、AE分别于点M、N.
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥BC,过BC作平面交AP、AE分别于点M、N.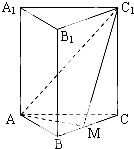 如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.
如图,正三棱柱ABC-A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.