Question

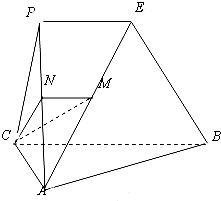如图，平面PAC⊥平面ABC，AC⊥BC，△PAC为等边三角形，PE∥BC，过BC作平面交AP、AE分别于点M、N．
（1）求证：MN∥PE；
（2）设

AN

AP

=λ，求λ 的值，使得平面ABC与平面MNC所成的锐二面角的大小为45°．

Answer 1

考点：与二面角有关的立体几何综合题

专题：空间位置关系与距离,空间角

分析：几何法：（Ⅰ）由PE∥CB，得BC∥平面APE，由此能证明MN∥PE．
（Ⅱ）由MN∥BC，得C、B、M、N共面，∠NCA为二面角N-CB-A的平面角，由此利用正弦定理能求出λ的值．
向量法：（1）以点C为原点建立空间直角坐标系C-xyz，利用向量法能证明MN∥平面ABC．
（2）分别求出平面CMN的法向量和平面ABC的法向量，由此利用向量法能求出λ=

3

-1．

解答： 几何法：
（Ⅰ） 证明：因为PE∥CB，所以BC∥平面APE  …（3分）
又依题意平面ABC交平面APE于MN，
故MN∥BC，
所以MN∥PE．…（6分）
（Ⅱ）解：由（Ⅰ）知MN∥BC，故C、B、M、N共面，
平面ABC与平面MNC所成的锐二面角即N-CB-A．
因为平面PAC⊥平面ABC，
平面PAC∩平面ABC=AC，且CB⊥AC，
所以CB⊥平面PAC．故CB⊥CN，
故∠NCA为二面角N-CB-A的平面角…（10分）
所以∠NCA=45°．
在△NCA中运用正弦定理得

AN

AC

=

sin45°

sin75°

=

2 2

6 + 2 4

=

3

-1．
所以λ=

AN

AP

=

3

-1．…（14分）
向量法：
（1）证明：如图以点C为原点建立 空间直角坐标系C-xyz，
不妨设CA=1，CB=t（t＞0），

PE

=μ

CB

，
则C（0，0，0），A（1，0，0），B（0，t，0），P(

1

2

 ， 0 ， 

3

2

)，E(

1

2

 ， μt ， 

3

2

)．
由

AM

AE

=

AN

AP

=λ，得M(1-

1

2

λ ， λμt ， 

3

2

λ)，
N(1-

1

2

λ ， 0 ， 

3

2

λ)，

MN

=(0 ， -λμt ， 0)．

n0

=（0，0，1）是平面ABC的一个法向量，
且

n0

•

MN

=0，故

n0

⊥

MN

．
又因为MN?平面ABC，即知MN∥平面ABC．…（6分）
（2）解：

MN

=(0 ， -λμt ， 0)，

CM

=(1-

1

2

λ ， λμt ， 

3

2

λ)，
设平面CMN的法向量

n1

=(x1 ， y1 ， z1)，
则

n1

•

MN

=0，

n1

•

CM

=0，可取

n1

=(1 ， 0 ，

λ-2

3 λ

)，
又

n0

=（0，0，1）是平面ABC的一个法向量．
由|cosθ|=

| n0 • n1 |

| n0 |•| n1 |

，
以及θ=45°得

| λ-2 3 λ |

1+ (λ-2)2 3λ2

=

2

2

，
即2λ²+4λ-4=0．解得λ=

3

-1（将λ=-1-

3

舍去），
故λ=

3

-1．…（14分）

点评：本题考查直线与直线平行的证明，考查使锐二面角的大小为45°的实数值的求法，解题时要认真审题，注意空间思维能力的培养．