题目内容
11.设a=${∫}_{0}^{\frac{π}{2}}$(sinx+cosx)dx,则二项式(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6展开式中含x-1项的系数是60.分析 由定积分的运算求得a的值,代入求得(2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6展开式${C}_{6}^{k}$(2$\sqrt{x}$)6-k•(-$\frac{1}{\sqrt{x}}$)k=(-1)k${C}_{6}^{k}$26-kx3-k,当3-k=-1,解得k=4,代入即可求得展开式中含x-1项的系数.
解答 解:a=${∫}_{0}^{\frac{π}{2}}$(sinx+cosx)dx=(-cosx+sinx)${丨}_{0}^{\frac{π}{2}}$
=-(cos$\frac{π}{2}$-cos0)+sin$\frac{π}{2}$-sin0=2,∴a=2,
(2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)6展开式为:${C}_{6}^{k}$(2$\sqrt{x}$)6-k•(-$\frac{1}{\sqrt{x}}$)k=(-1)k${C}_{6}^{k}$26-kx3-k,
含x-1项的系数:3-k=-1,解得:k=4,
∴展开式中含x-1项的系数(-1)k${C}_{6}^{k}$26-kx3-k,
=(-1)4${C}_{6}^{2}$22,
=60,
故答案为:60.
点评 本题考查定积分的应用,考查二项式定理,考查计算能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
1.用数学归纳法证明$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+…$\frac{1}{2n}$<1(n∈N*且n>1)由n=k到n=k+1时,不等式左边应添加的项是( )
| A. | $\frac{1}{2(k+1)}$ | B. | $\frac{1}{2k+1}$+$\frac{1}{2k+2}$-$\frac{1}{k}$ | ||
| C. | $\frac{1}{2k+1}$+$\frac{1}{2k+2}$-$\frac{1}{k+1}$ | D. | $\frac{1}{2k+1}$+$\frac{1}{2k+2}$-$\frac{1}{k+1}$-$\frac{1}{k+2}$ |
2.设函数f(x)=sin(2x+φ)+cos(2x+φ)(|φ|<$\frac{π}{2}$)为偶函数,则φ=( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
3.已知y=f(x)为R上的连续可导的奇函数,当x>0时f′(x)+$\frac{f(x)}{x}$<0,则g(x)=f(x)+$\frac{2}{x}$的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
1.正三角形ABC的边长为1,设$\overrightarrow{AB}$=$\vec a$,$\overrightarrow{BC}$=$\vec b$,$\overrightarrow{AC}$=$\vec c$,那么$\vec a$•$\vec b$+$\vec b$•$\vec c$+$\vec c$•$\vec a$的值是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{1}{2}$ |
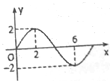 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)=$\sqrt{2}$.
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)=$\sqrt{2}$.