题目内容
已知等差数列{an}的前n项和为Sn，且a2=8，S4=40．数列{bn}的前n项和为Tn，且Tn-2bn+3=0，n∈N*．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）设cn=
，求数列{cn}的前2n+1项和P2n+1．
（Ⅰ）求数列{an}，{bn}的通项公式；
（Ⅱ）设cn=
|
考点：数列的求和
专题：计算题,等差数列与等比数列
分析：（Ⅰ）运用等差数列的通项公式与求和公式，根据条件列方程，求出首项和公差，得到通项an，运用n=1时，b1=T1，n＞1时，bn=Tn-Tn-1，求出bn；
（Ⅱ）写出cn，然后运用分组求和，一组为等差数列，一组为等比数列，分别应用求和公式化简即可．
（Ⅱ）写出cn，然后运用分组求和，一组为等差数列，一组为等比数列，分别应用求和公式化简即可．
解答：
解：（Ⅰ）设等差数列{an}的公差为d，
由题意，得
，解得
，
∴an=4n；
∵Tn-2bn+3=0，∴当n≥2时，Tn-1-2bn-1+3=0，
两式相减，得bn=2bn-1，（n≥2）
又当n=1时，b1=3，
则数列{bn}为等比数列，
∴bn=3•2n-1；
（Ⅱ）cn=
∴P2n+1=（a1+a3+…+a2n+1）+（b2+b4+…+b2n）
=
•(n+1)+
=22n+1+4n2+8n+2．
由题意，得
|
|
∴an=4n；
∵Tn-2bn+3=0，∴当n≥2时，Tn-1-2bn-1+3=0，
两式相减，得bn=2bn-1，（n≥2）
又当n=1时，b1=3，
则数列{bn}为等比数列，
∴bn=3•2n-1；
（Ⅱ）cn=
|
∴P2n+1=（a1+a3+…+a2n+1）+（b2+b4+…+b2n）
=
| 4+4(2n+1) |
| 2 |
| 6(1-4n) |
| 1-4 |
=22n+1+4n2+8n+2．
点评：本题主要考查等差数列和等比数列的通项与前n项和公式，考查方程在数列中的运用，考查数列的求和方法：分组求和，必须掌握．
练习册系列答案
相关题目
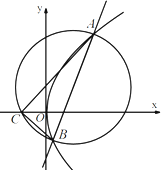已知抛物线的顶点为（0，0），准线为x=-2，不垂直于x轴的直线x=ty+1与该抛物线交于A，B两点，圆M以AB为直径． 
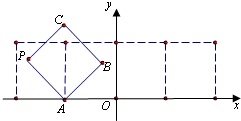如图放置的边长为1的正方形PABC沿x轴滚动，点B恰好经过原点．设顶点P（x，y）的轨迹方程是y=f（x），则对函数y=f（x）有下列判断：