题目内容
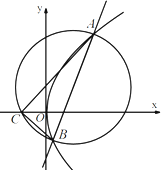 已知抛物线的顶点为(0,0),准线为x=-2,不垂直于x轴的直线x=ty+1与该抛物线交于A,B两点,圆M以AB为直径.
已知抛物线的顶点为(0,0),准线为x=-2,不垂直于x轴的直线x=ty+1与该抛物线交于A,B两点,圆M以AB为直径. (Ⅰ)求抛物线的方程;
(Ⅱ)圆M交x轴的负半轴于点C,是否存在实数t,使得△ABC的内切圆的圆心在x轴上?若存在,求出t的值;若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设抛物线方程为y2=ax,由准线为x=-2,能求出抛物线方程.
(Ⅱ)设A(x1,y1),B(x2y2),C(x0,0),由
,得:y2-8ty-8=0,由此利用韦达定理能求出t的值.
(Ⅱ)设A(x1,y1),B(x2y2),C(x0,0),由
|
解答:
解:(Ⅰ)设抛物线方程为y2=ax,
又a=2×4=8,
∴抛物线方程为y2=8x.…(3分)
(Ⅱ)设A(x1,y1),B(x2y2),C(x0,0)
由
,得:y2-8ty-8=0,…(5分)
则
,
由点C在以AB为直径的圆上得,
•
=0.…(7分)
又
=(x1-x0,y1-0),
=(x2-x0,y2-0),
∴(x1-x0)(x2-x0)+y1y2=0,
又x1=ty1+1,x2=ty2+1,
∴
-(t(y1+y2)+2)x0+
+y1y2=0,
∴
-(8t2+2)x0-7=0(*),…(9分)
若存在t,使得△ABC的内心在x轴上,
则kCA+kCB=0…(12分)
∴
+
=0,
即2ty1y2+(y1+y2)(1-x0)=0,
即2t(-8)+8t(1-x0)=0,
∴x0=-1.…(14分)
结合(*)得,t=±
.…(15分)
又a=2×4=8,
∴抛物线方程为y2=8x.…(3分)
(Ⅱ)设A(x1,y1),B(x2y2),C(x0,0)
由
|
则
|
由点C在以AB为直径的圆上得,
| CA |
| CB |
又
| CA |
| CB |
∴(x1-x0)(x2-x0)+y1y2=0,
又x1=ty1+1,x2=ty2+1,
∴
| ||||
| 64 |
| x | 2 0 |
∴
| x | 2 0 |
若存在t,使得△ABC的内心在x轴上,
则kCA+kCB=0…(12分)
∴
| y1 |
| x1-x0 |
| y2 |
| x2-x0 |
即2ty1y2+(y1+y2)(1-x0)=0,
即2t(-8)+8t(1-x0)=0,
∴x0=-1.…(14分)
结合(*)得,t=±
| ||
| 2 |
点评:本题考查抛物线方程的求法,考查满足条件的实数是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
与角-80°终边相同的角是( )
| A、80° | B、100° |
| C、260° | D、280° |
设a∈R,则“a=-1”是“直线ax+y-1=0与直线x+y+5=0垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
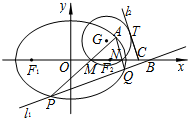 已知椭圆E:x2+2y2=6 的两个焦点为F1、F2,A是椭圆上位于第一象限的一点,△AF1F2的面积为
已知椭圆E:x2+2y2=6 的两个焦点为F1、F2,A是椭圆上位于第一象限的一点,△AF1F2的面积为