题目内容
已知函数f(x)=ax2+bx+c(a>0)满足f(0)=-1,方程f(x)=x-1只有一个根,且f(-
+x)=f(-
-x)
(1)求函数f(x)的解析式;
(2)是否存在实数a,使函数g(x)=log
(f(a))x在(-∞,+∞)上为减函数?若存在,求出实数a的取值范围;若不存在,说明理由.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求函数f(x)的解析式;
(2)是否存在实数a,使函数g(x)=log
| 1 |
| 2 |
考点:复合函数的单调性
专题:函数的性质及应用
分析:(1)根据二次函数的性质建立方程条件即可求函数f(x)的解析式;
(2)根据复合函数单调性之间的关系,即可得到结论.
(2)根据复合函数单调性之间的关系,即可得到结论.
解答:
解:(1)∵函数f(x)=ax2+bx+c(a>0)满足f(0)=-1,
∴f(0)=c=-1,
∵f(-
+x)=f(-
-x),
∴函数关于x=-
对称,
则x=-
=-
,即a=b,
则f(x)=ax2+ax-1,
则f(x)=x-1,即ax2+ax-1=x-1,
则ax2+(a-1)x=0,
∵f(x)=x-1只有一个根,
∴△=(a-1)2-0=0,
解得a=1,则b=1,
即函数f(x)的解析式为f(x)=x2+x-1;
(2)若存在实数a,使函数g(x)=log
(f(a))x在(-∞,+∞)上为减函数,
则根据复合函数单调性之间的关系可知函数y=f(a)x在(-∞,+∞)上为增函数,
即f(a)=a2+a-1>1,即a2+a-2>0;
解得a>1或a<-2,
即当a>1或a<-2时,函数g(x)=log
[(f(a)]x在(-∞,+∞)上为减函数.
∴f(0)=c=-1,
∵f(-
| 1 |
| 2 |
| 1 |
| 2 |
∴函数关于x=-
| 1 |
| 2 |
则x=-
| b |
| 2a |
| 1 |
| 2 |
则f(x)=ax2+ax-1,
则f(x)=x-1,即ax2+ax-1=x-1,
则ax2+(a-1)x=0,
∵f(x)=x-1只有一个根,
∴△=(a-1)2-0=0,
解得a=1,则b=1,
即函数f(x)的解析式为f(x)=x2+x-1;
(2)若存在实数a,使函数g(x)=log
| 1 |
| 2 |
则根据复合函数单调性之间的关系可知函数y=f(a)x在(-∞,+∞)上为增函数,
即f(a)=a2+a-1>1,即a2+a-2>0;
解得a>1或a<-2,
即当a>1或a<-2时,函数g(x)=log
| 1 |
| 2 |
点评:本题主要考查二次函数解析式的求解以及复合函数单调性的判断,综合性较强.

练习册系列答案
相关题目
某校举行的数学建模比赛,全体参赛学生的比赛成绩ξ近似服从正态分布N(70,σ2),(σ>0),参赛学生共600名.若ξ在(70,90)内的取值概率为0.48,那么90分以上(含90分)的学生人数为 .
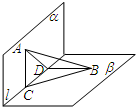 已知平面α⊥平面β,α∩β=l,A∈α,B∈β,AC⊥l,垂足为C,BD⊥l,垂足为D(点C,D不重合),若AC>BD,则( )
已知平面α⊥平面β,α∩β=l,A∈α,B∈β,AC⊥l,垂足为C,BD⊥l,垂足为D(点C,D不重合),若AC>BD,则( )| A、AD>BC,∠ABC>∠BAD |
| B、AD>BC,∠ABC<∠BAD |
| C、AD<BC,∠ABC>∠BAD |
| D、AD<BC,∠ABC<∠BAD |
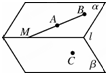 如图,α∩β=l,A,B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )
如图,α∩β=l,A,B∈α,C∈β,且C∉l,直线AB∩l=M,过A,B,C三点的平面记作γ,则γ与β的交线必通过( )| A、点A | B、点B |
| C、点C但不过点M | D、点C和点M |