题目内容
7.某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1-50号,并分组,第一组1-5号,第二组6-10号,…,第十组45-50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为37的学生.分析 由题设知第八组的号码数比第三组的号码数大(8-3)×5,由此能求出结果
解答 解:这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,
在第三组中抽得号码为12的学生,
则在第八组中抽得号码为12+(8-3)×5=37.
故答案为:37.
点评 抽样选用哪一种抽样形式,要根据题目所给的总体情况来决定,若总体个数较少,可采用抽签法,若总体个数较多且个体各部分差异不大,可采用系统抽样,若总体的个体差异较大,可采用分层抽样

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.三角形的面积为S=$\frac{1}{2}$(a+b+c)•r,(a,b,c为三角形的边长,r为三角形的内切圆的半径)利用类比推理,可以得出四面体的体积为( )
| A. | V=$\frac{1}{3}$abc(a,b,c,为底面边长) | |
| B. | V=$\frac{1}{3}$Sh(S为底面面积,h为四面体的高) | |
| C. | V=$\frac{1}{3}$(S1+S2+S3+S4)r(S1,S2,S3,S4分别为四面体四个面的面积,r为四面 体内切球的半径) | |
| D. | V=$\frac{1}{3}$(ab+bc+ac)h(a,b,c为底面边长,h为四面体的高) |
12.正四棱柱ABCD-A1B1C1D1中,底面边长为2,侧棱长为4,则B1点到平面AD1C的距离为( )
| A. | $\frac{8}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{4}{3}$ |
19.数列{an}中,已知对任意自然数n,a1+a2+a3+…+an=2n,则a12+a22+a32+…+an2=( )
| A. | $\frac{1}{3}$(4n-1) | B. | $\frac{1}{3}$(2n-1) | C. | 4n-1 | D. | $\frac{1}{3}$(4n+8) |
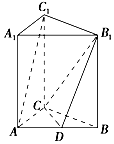 如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.