题目内容
15.已知角α的终边经过点P(-4a,3a)(a≠0),求sinα+cosα-tanα的值.分析 利用任意角的三角函数的定义,分类讨论求得sinα+cosα-tanα的值.
解答 解:由题意,x=-4a,y=3a,r=|5a|.
当a>0时,sinα+cosα-tanα=$\frac{3}{5}$-$\frac{4}{5}$+$\frac{3}{4}$=$\frac{11}{20}$,
当a<0时,sinα+cosα-tanα=-$\frac{3}{5}$+$\frac{4}{5}$+$\frac{3}{4}$=$\frac{19}{20}$.
点评 本题主要考查任意角的三角函数的定义,属于基础题.

练习册系列答案
相关题目
20.下列函数中,在(0,$\frac{π}{2}$)上是增函数的偶函数是( )
| A. | y=|sinx| | B. | y=|sin2x| | C. | y=|cosx| | D. | y=tanx |
4.已知{an}为等差数列,若a1+a2+a3=$\frac{π}{2}$,a7+a8+a9=π,则cosa5的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
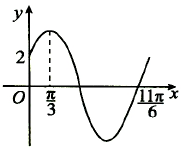 已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(ω>0,0<φ<\frac{π}{2})$的部分图象如图所示.