题目内容
设f（x）是定义在R上的函数，且f（x+3）=-f（x），f（-1）=2，则f（2012）= ．
考点：周期函数,函数的值
专题：函数的性质及应用
分析：由已知中f（x+3）=-f（x），f（-1）=2，可得f（2）=-2，且f（x）是以6为周期的周期函数，结合2012=335×6+2，可得f（2012）=f（2）．
解答：
解：∵f（x+3）=-f（x），f（-1）=2，
∴f（-1+3）=f（2）=-f（-1）=-2，
且f（x+6）=-f（x+3）=f（x），
即f（x）是以6为周期的周期函数，
∵2012=335×6+2，
∴f（2012）=f（2）=-2，
故答案为：-2．
∴f（-1+3）=f（2）=-f（-1）=-2，
且f（x+6）=-f（x+3）=f（x），
即f（x）是以6为周期的周期函数，
∵2012=335×6+2，
∴f（2012）=f（2）=-2，
故答案为：-2．
点评：本题考查的知识点是函数的周期性，函数求值，其中分析出f（x）是以6为周期的周期函数，是解答的关键．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
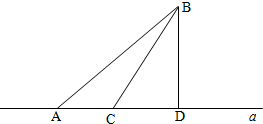如图，某海滨浴场的岸边可近似地看作直线a，救生员现在岸边的A处，发现海中的B处有人求救，救生员没有直接从A处游向B处，而是在AD（D为海岸边距B最近的点）上找到一点C，沿岸边从A处跑到C处，然后游到B处，若救生员在岸边的行进速度为4（m/s），在海水中的行进速度为2（m/s），∠BAD=45°，BD=200（m），救生员从A到C再到B的时间为y（s）．