题目内容
不等式组
所表示的平面区域是面积为1的直角三角形,则z=x-2y的最大值是( )
|
| A、-5 | B、-2 | C、-1 | D、1 |
考点:简单线性规划
专题:不等式的解法及应用
分析:先求出k的值,从而画出满足条件的平面区域,由z=x-2y得:y=
x-
,从而求出z的最大值.
| 1 |
| 2 |
| z |
| 2 |
解答:
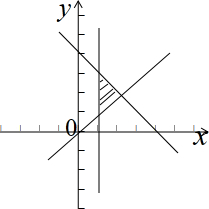 解:∵区域是直角三角形,因此直线 x+y-4=0 与 kx-y=0 的斜率之积等于-1,
解:∵区域是直角三角形,因此直线 x+y-4=0 与 kx-y=0 的斜率之积等于-1,
即 (-1)•k=-1,
解得 k=1,而当 k=1 时区域面积恰为 1,
画出满足条件的平面区域,
如图示:
由z=x-2y得:y=
x-
,
联立
,解得:
,
∴y=
x-
过(1,1)时,-
取到最小值,z取到最大值,
∴Z最大值=1-2=-1,
故选:C.
 解:∵区域是直角三角形,因此直线 x+y-4=0 与 kx-y=0 的斜率之积等于-1,
解:∵区域是直角三角形,因此直线 x+y-4=0 与 kx-y=0 的斜率之积等于-1,即 (-1)•k=-1,
解得 k=1,而当 k=1 时区域面积恰为 1,
画出满足条件的平面区域,
如图示:
由z=x-2y得:y=
| 1 |
| 2 |
| z |
| 2 |
联立
|
|
∴y=
| 1 |
| 2 |
| z |
| 2 |
| z |
| 2 |
∴Z最大值=1-2=-1,
故选:C.
点评:本题考查了简单的线性规划问题,考查了数形结合思想,是一道中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设曲线y=ax3在点(1,a)处的切线与直线6x-y+2=0平行,则a=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
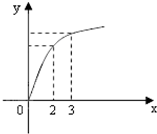 已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )
已知函数f(x)的图象如图所示,f′(x)是f(x)的导函数,则下列数值排序正确的是( )| A、f′(2)<f′(3)<f(3)-f(2) |
| B、f′(3)<f(3)-f(2)<f′(2) |
| C、f′(3)<f′(2)<f(3)-f(2) |
| D、f(3)-f(2)<f′(2)<f′(3) |
已知等差数列{an}共有10项,并且其偶数项之和为30,奇数项之和为25,由此得到的结论正确的是( )
| A、d=1 | ||
B、d=
| ||
| C、a6=5 | ||
| D、a6=-5 |
已知一个程序框图如图所示,若输入n=6,则该程序运行的结果是( )


| A、2 | B、3 | C、4 | D、15 |
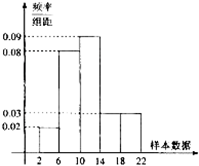 样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的
样本容量为200的频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在[6,10)内的