题目内容

18．哈市某公司有五个不同部门，现有4名在校大学生来该公司实习，要求安排到该公司的两个部门，且每部门安排两名，则不同的安排方案种数为（　　）
A．40B．60C．120D．240

分析 本题是一个计数问题，由题意可知，可分两步完成计数，先对四名大学生分组，分法有$\frac{1}{2}{C}_{4}^{2}$种，然后再排到5个部门的两个部门中，排列方法有A52，计算此两数的乘积即可得到不同的安排方案种数，再选出正确选项

解答 解：此问题可分为两步求解，第一步将四名大学生分为两组，由于分法为2，2，考虑到重复一半，故分组方案应为$\frac{1}{2}{C}_{4}^{2}$种，
第二步将此两组大学生分到5个部门中的两个部门中，不同的安排方式有A52，
故不同的安排方案有$\frac{1}{2}{C}_{4}^{2}$A52=60种，
故选：B．

点评 本题考查排列组合及简单计数问题，解题的关键是理解事件“某公司共有5个部门，有4名大学毕业生，要安排到该公司的两个部门且每个部门安排2名，”将问题分为两步来求解．

练习册系列答案
相关题目
10．已知集合A={x||x+1|≥1}，B={x|x≥-1}，则（∁RA）∩B=（　　）
A．[-1，0]B．[-1，0）C．（-2，-1）D．（-2，-1]
9．设命题p：实数k满足：方程$\frac{{x}^{2}}{k-1}$+$\frac{{y}^{2}}{7-a}$=1表示焦点在y轴上的椭圆；
命题q，实数k满足：方程（4-k）x2+（k-2）y2=1不表示双曲线．
（1）若命题q为真命题，求k的取值范围；
（2）若p是q的必要不充分条件，求实数a的取值范围．
6．函数f（x）=$\sqrt{3}$sinωxcosωx+cos2ωx（ω＞0）（ω＞0）在区间[$\frac{π}{6}$，$\frac{π}{3}$]的值域是[-$\frac{1}{2}$，$\frac{1}{2}$]，则常数ω所有可能的值的个数是（　　）
A．0B．1C．2D．4
13．等差数列{an}的公差d≠0，且a3，a5，a15成等比数列，若a1=3，Sn为数列an的前n项和，则Sn的最大值为（　　）
A．8B．6C．5D．4
3．已知a＞0，b＞0，则$\frac{{a}^{2}+4+4ab+4{b}^{2}}{a+2b}$的最小值为（　　）
A．$\frac{1}{4}$B．1C．2D．4
10．设△ABC的内角A、B、C的对边分别为a、b、c，且满足sinA+sinB=[cosA-cos（π-B）]•sinC．
（1）试判断△ABC的形状，并说明理由；
（2）若a+b+c=1+$\sqrt{2}$，试求△ABC面积的最大值．
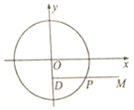7．如图，已知DP⊥y轴，点D为垂足，点M在线段DP的延长线上，且满足|DP|=|PM|，当点P在圆x2+y2=3上运动时
（1）求点M的轨迹C的方程；
（2）直线l：x=my+3（m≠0）交曲线C于A、B两点，设点B关于x轴的对称点为B1（点B1与点A不重合），且直线B1A与x轴交于点E．
①证明：点E是定点；
②△EAB的面积是否存在最大值？若存在，求出最大值，若不存在，请说明理由．
8．已知实数x，y满足条件$\left\{\begin{array}{l}{x≥2}\\{x+y≤4}\\{-2x+y+m≥0}\end{array}\right.$若目标函数z=2x+y的最小值为3，则其最大值为7．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网