题目内容
10.已知集合A={x||x+1|≥1},B={x|x≥-1},则(∁RA)∩B=( )| A. | [-1,0] | B. | [-1,0) | C. | (-2,-1) | D. | (-2,-1] |
分析 求解绝对值的不等式化简A,再由交、并、补集的混合运算得答案.
解答 解:∵A={x||x+1|≥1}={x|x≤-2或x≥0},
∴∁RA={x|-2<x<0},又B={x|x≥-1},
∴(∁RA)∩B=[-1,0).
故选:B.
点评 本题考查绝对值不等式的解法,考查交、并、补集的混合运算,是基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
1. 如图,四面体ABCD中,E,F分别是AC,BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成角的度数为( )
如图,四面体ABCD中,E,F分别是AC,BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成角的度数为( )
 如图,四面体ABCD中,E,F分别是AC,BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成角的度数为( )
如图,四面体ABCD中,E,F分别是AC,BD的中点,若CD=2AB=4,EF⊥AB,则EF与CD所成角的度数为( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
5.某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是( )


| A. | 圆弧 | B. | 抛物线的一部分 | C. | 椭圆的一部分 | D. | 双曲线的一部分 |
15.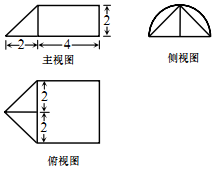 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{8}{3}$+8π | B. | $\frac{16}{3}$+8π | C. | $\frac{8}{3}$+16π | D. | $\frac{16}{3}$+16π |
19.执行如图所示的程序框图,则输出S的值是( )
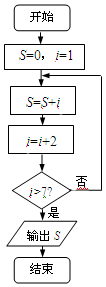

| A. | 9 | B. | 16 | C. | 25 | D. | 27 |
18.哈市某公司有五个不同部门,现有4名在校大学生来该公司实习,要求安排到该公司的两个部门,且每部门安排两名,则不同的安排方案种数为( )
| A. | 40 | B. | 60 | C. | 120 | D. | 240 |