题目内容
13.等差数列{an}的公差d≠0,且a3,a5,a15成等比数列,若a1=3,Sn为数列an的前n项和,则Sn的最大值为( )| A. | 8 | B. | 6 | C. | 5 | D. | 4 |
分析 设出等差数列的公差,由a3,a5,a15成等比数列建立关系式,用a1=3和公差d表示出a3,a5,a15求解d,求解数列an的前n项和Sn可得最大值
解答 解:设等差数列的公差为d,a1=3,
∴a3=3+2d,a5=3+4d,a15=3+14d,
由a3,a5,a15成等比数列,
可得(3+4d)2=(3+2d)(3+14d),
∵d≠0
解得:d=-2,
∴Sn=$3n+\frac{n(n-1)}{2}×(-2)$=4n-n2.
当n=2时,Sn最大为4.
故选:D.
点评 本题考查了等差数列的通项公式,考查了等差数列的前n项和,是基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是( )


| A. | 圆弧 | B. | 抛物线的一部分 | C. | 椭圆的一部分 | D. | 双曲线的一部分 |
4.已知二次函数y=f(x)的图象向上平移2个单位长度,再向右平移1个单位长度,得到函数y=-2x2+4x+1的图象,则f(x)的函数解析式为( )
| A. | f(x)=-2x2+1 | B. | f(x)=-2(x+1)2+2 | C. | f(x)=-2(x-3)2+4 | D. | f(x)=-2(x-2)2+5 |
18.哈市某公司有五个不同部门,现有4名在校大学生来该公司实习,要求安排到该公司的两个部门,且每部门安排两名,则不同的安排方案种数为( )
| A. | 40 | B. | 60 | C. | 120 | D. | 240 |
3.已知集合A={x|x2-2x-3>0},B={x|lg(x-2)≤1},则(∁RA)∪B=( )
| A. | (-1,12) | B. | (2,3) | C. | (2,3] | D. | [-1,12] |
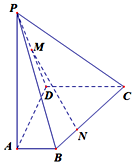 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$. 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有42株树木的底部周长小于110cm.
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有42株树木的底部周长小于110cm.