题目内容
10.设△ABC的内角A、B、C的对边分别为a、b、c,且满足sinA+sinB=[cosA-cos(π-B)]•sinC.(1)试判断△ABC的形状,并说明理由;
(2)若a+b+c=1+$\sqrt{2}$,试求△ABC面积的最大值.
分析 (1)由诱导公式、正弦定理和余弦定理化简已知的式子,化简后由边的关系判断出三角形的形状;
(2)由(1)和条件化简后,由基本不等式化简求出$\sqrt{ab}$的范围,表示三角形的面积,即可求出答案.
解答 解:(1)∵sinA+sinB=[cosA-cos(π-B)]•sinC,
∴sinA+sinB=(cosA+cosB)•sinC,
由正弦定理和余弦定理得,
a+b=($\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$+$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$)•c,
化简得,2a2b+2ab2=ab2+ac2-a3+ba2+bc2-b3
a2b+ab2=ac2-a3+bc2-b3,
(a+b)(a2+b2-c2)=0,
又a+b>0,∴a2+b2-c2=0,即a2+b2=c2,
∴△ABC为直角三角形,且∠C=90°;
(2)∵a+b+c=1+$\sqrt{2}$,a2+b2=c2,
∴1+$\sqrt{2}$=a+b+$\sqrt{{a}^{2}+{b}^{2}}$≥2$\sqrt{ab}$+$\sqrt{2ab}$=(2+$\sqrt{2}$)•$\sqrt{ab}$
当且仅当a=b时上式等号成立,则$\sqrt{ab}$≤$\frac{1+\sqrt{2}}{2+\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
∴S△ABC=$\frac{1}{2}$ab≤$\frac{1}{2}$×$(\frac{\sqrt{2}}{2})^{2}$=$\frac{1}{4}$,
即△ABC面积的最大值为$\frac{1}{4}$.
点评 本题考查正弦定理、余弦定理的应用:角化边,以及基本不等式求三角形面积最值中的应用,考查转化思想,化简、变形能力.

| A. | 40 | B. | 60 | C. | 120 | D. | 240 |
| A. | $\frac{9}{2}$ | B. | $\frac{9}{4}$ | C. | 1 | D. | 9 |
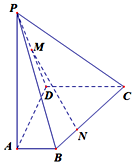 如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$.
如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD是直角梯形,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点M为PD的中点,点N是为棱CB上一点,且$\overrightarrow{BN}=λ\overrightarrow{BC},λ∈({0,1})$. 为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有42株树木的底部周长小于110cm.
为了了解一片经济林的生长情况,随机抽测了其中60株树木的底部周长(单位:cm),所得数据均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有42株树木的底部周长小于110cm.