题目内容
已知P(a,b)是直线x+2y-1=0上任一点,求S=
的最小值.
| a2+b2+4a-6b+13 |
考点:点到直线的距离公式
专题:圆锥曲线的定义、性质与方程
分析:由已知条件推导出S=
的最小值等于点(-2,3)到直线x+2y-1=0的距离,由此能求出结果.
| a2+b2+4a-6b+13 |
解答:
解:∵P(a,b)是直线x+2y-1=0上任一点,
∴a+2b-1=0,
∴S=
=
,
∴S=
的最小值Smin
等于点(-2,3)到直线x+2y-1=0的距离,
∴Smin=
=
.
∴S=
的最小值是
.
∴a+2b-1=0,
∴S=
| a2+b2+4a-6b+13 |
| (a+2)2+(b-3)2 |
∴S=
| a2+b2+4a-6b+13 |
等于点(-2,3)到直线x+2y-1=0的距离,
∴Smin=
| |-2+6-1| | ||
|
3
| ||
| 5 |
∴S=
| a2+b2+4a-6b+13 |
3
| ||
| 5 |
点评:本题考查最小值的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
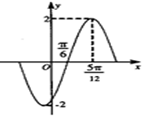 已知函数f(x)=Msin(ωx+φ)(x∈R,M>0,ω>0,|φ|<
已知函数f(x)=Msin(ωx+φ)(x∈R,M>0,ω>0,|φ|<