题目内容
已知1，a1，a2，9四个实数成等差数列，1，b1，b2，b3，9五个数成等比数列，则b2（a2-a1）等于（ ）
| A、8 | ||
| B、-8 | ||
| C、±8 | ||
D、
|
考点：等比数列的性质,等差数列的性质
专题：计算题,等差数列与等比数列
分析：设等差数列的公差为d，比数列的公比为q，由题意可得d和q，代入要求的式子化简可得．
解答：
解：设等差数列的公差为d，等比数列的公比为q，
则有1+3d=9，1•q4=9，
解之可得d=
，q2=3，
∴b2（a2-a1）=1×q2×
=8．
故选：A．
则有1+3d=9，1•q4=9，
解之可得d=
| 8 |
| 3 |
∴b2（a2-a1）=1×q2×
| 8 |
| 3 |
故选：A．
点评：本题考查等比数列和等差数列的性质和应用，解题时要认真审题，注意等比数列和等差数列的通项公式的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
已知3，a，13成等差数列，实数c，9，27成等比数列，则a+c的值是（ ）
| A、11 | B、12 | C、13 | D、14 |
当你到一个红绿灯路口时，红灯的时间为30秒，黄灯的时间为5秒，绿灯的时间为45秒，那么你看到黄灯的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
使不等式
+
＞1+
成立的正整数a的最大值是（ ）
| 3 |
| 8 |
| a |
| A、10 | B、11 | C、12 | D、13 |
已知cosα=
，且0＜α＜π，则tan（α+
）=（ ）
| 4 |
| 5 |
| π |
| 4 |
A、
| ||
| B、7 | ||
C、-
| ||
| D、-7 |
已知函数f（x）=
，则f（f（-2））=（ ）
|
| A、2 | B、1 | C、-2 | D、-1 |
一批产品中，有10件正品和5件次品，对产品逐个进行检测，如果已检测到前3次均为正品，则第4次检测的产品仍为正品的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
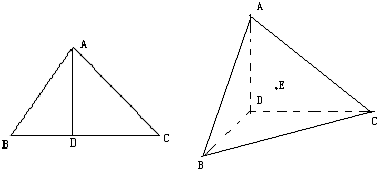如图，∠ACB=45°，BC=6过A作AD⊥BC，垂足D在线段BC上且异于点B，沿AD将△ABD折起，组成三棱锥A-BCD，过点D作DE⊥平面ABC，且点E为三角形ABC的垂心．