题目内容
5．设|a|＜1，函数f（x）=ax2+x-a（-1≤x≤1），证明：|f（x）|≤$\frac{5}{4}$．分析 利用绝对值不等式，结合配方法，即可证明结论．
解答 证明：∵|f（x）|=|a（x2-1）+x|≤|a（x2-1）|+|x|≤|x2-1|+|x|=1-x2+|x|=-（|x|-$\frac{1}{2}$）2+$\frac{5}{4}$≤$\frac{5}{4}$，
∴|f（x）|≤$\frac{5}{4}$．
点评 本题考查不等式的证明，考查绝对值不等式的运用，属于中档题．
练习册系列答案
相关题目
15．在区间[0，1]上随机选取两个数x和y，则y＞2x的概率为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{3}$ |
16．在直三棱柱ABC-A1BlC1中，平面α与棱AB，AC，A1C1，A1B1分别交于点E，F，G，H，且直线AA1∥平面α．有下列三个命题：①四边形EFGH是平行四边形；②平面α∥平面BCC1B1；③平面α⊥平面BCFE．其中正确的命题有（ ）
| A． | ①② | B． | ②③ | C． | ①③ | D． | ①②③ |
13．宿州市日前提出，要提升市民的生活质量，改善民生，促进“中国梦”的实线，为此，某记者在街头随机采访了100名市民，根据他们对“中国梦”实线的信心情况进行统计分析，得到如下分布表：
（Ⅰ）以这100名市民信心指数为样本来估计市民的总体信心指数，若要从全市市民中随机任选3人进行信心跟踪，记ξ表示抽到信心级别为“非常有信心或有信心”市民人数，求ξ的分布列及期望；
（Ⅱ）从这100名市民中，任选两人，记他们的信心指数分别为m、n，求|m-n|≥60的概率．
| 信心级别 | 非常有信心 | 有信心 | 不知道 | 没信心 |
| 信心指数（分数） | 90 | 60 | 30 | 6 |
| 人数（名） | 42 | 38 | 14 | 6 |
（Ⅱ）从这100名市民中，任选两人，记他们的信心指数分别为m、n，求|m-n|≥60的概率．
20．执行如图所示的程序框图，则输出S的值为（ ）
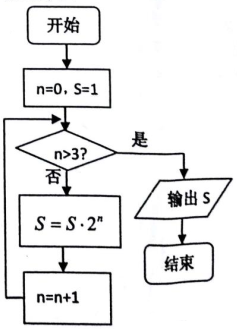
| A． | 16 | B． | 32 | C． | 64 | D． | 1024 |
10．已知函数$f（x）=\frac{1}{3}m{x^3}+\frac{1}{2}n{x^2}+x+2017$，其中m∈{2，4，6，8}，n∈{1，3，5，7}，从这些函数中任取不同的两个函数，在它们在（1，f（1））处的切线相互平行的概率是（ ）
| A． | $\frac{7}{120}$ | B． | $\frac{7}{60}$ | C． | $\frac{7}{30}$ | D． | 以上都不对 |
17．设抛物线x2=4y的焦点为F，过点F作斜率为k（k＞0）的直线l与抛物线相交于A、B两点，且点P恰为AB的中点，过点P作x轴的垂线与抛物线交于点M，若|MF|=4，则直线l的方程为（ ）
| A． | $y=2\sqrt{2}x+1$ | B． | $y=\sqrt{3}x+1$ | C． | $y=\sqrt{2}x+1$ | D． | $y=2\sqrt{3}x+2$ |
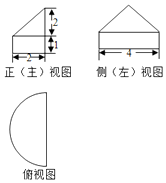
14．某几何体的三视图如图所示，其俯视图是由一个半圆与其直径组成的图形，则此几何体的体积是（ ）
| A． | 3π | B． | $\frac{10π}{3}$ | C． | $\frac{11π}{3}$ | D． | 4π |