题目内容
20. 如图,摄影爱好者在某公园A处发现正前方B处有一根立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为$\frac{π}{6}$,设摄影爱好者的眼睛(S)离地面的高度为$\sqrt{3}$m.
如图,摄影爱好者在某公园A处发现正前方B处有一根立柱,测得立柱顶端O的仰角和立柱底部B的俯角均为$\frac{π}{6}$,设摄影爱好者的眼睛(S)离地面的高度为$\sqrt{3}$m.(1)求摄影爱好者到立柱的水平距离和立柱的高度;
(2)立柱的顶端有一长2米的彩杆MN,绕其中点O在SA与立柱所在的平面内旋转.摄影爱好者有一视角范围为$\frac{π}{3}$的镜头,在彩杆转动的任意时刻,摄影爱好者是否都可以将彩杆全部摄入画面?说明理由.
分析 (1)摄影者眼部记为点S,作SC⊥OB于C,则有∠CSB=30°,∠ASB=60°.SA=$\sqrt{3}$,在Rt△SAB中,由三角函数的定义可求AB;再由SC=3,∠CSO=30°,在Rt△SCO中由三角函数的定义可求OC,进而可求OB
(2)以O为原点,以水平方向向右为x轴正方向建立平面直角坐标系.设M(cosθ,sinθ),θ∈[0,2π),则N(-cosθ,-sinθ),由(Ⅰ)知S(3,-$\sqrt{3}$),利用向量的数量积的坐标表示可求cos∠MSN∈[$\frac{11}{13}$,1],结合余弦函数的性质可求答案.
解答 解:(1)如图,不妨将摄影者眼部记为点S,作SC⊥OB于C,
依题意∠CSB=30°,∠ASB=60°.
又SA=$\sqrt{3}$,故在Rt△SAB中,可求得BA=$\frac{SA}{tan30°}$=3,
即摄影者到立柱的水平距离为3米.…(3分)
由SC=3,∠CSO=30°,在Rt△SCO中OC=SC•tan30°=$\sqrt{3}$,
又BC=SA=$\sqrt{3}$,故OB=2$\sqrt{3}$,即立柱的高度为2$\sqrt{3}$米.…(6分)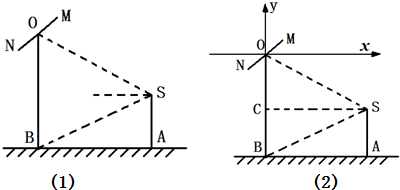
(2)如图,以O为原点,以水平方向向右为x轴正方向建立平面直角坐
标系.设M(cosθ,sinθ),θ∈[0,2π),
则N(-cosθ,-sinθ),由(1)知S(3,-$\sqrt{3}$).…(8分)
故$\overrightarrow{SM}$=(cosθ-3,sinθ+$\sqrt{3}$),$\overrightarrow{SN}$=(-$\sqrt{(-cosθ-3)^{2}+(-sinθ+\sqrt{3})^{2}}$=,-sinθ+$\sqrt{3}$),
∴$\overrightarrow{SM}$•$\overrightarrow{SN}$=(cosθ-3)(-cosθ-3)+(sinθ-$\sqrt{3}$)(-sinθ-$\sqrt{3}$)=11(10分)
|$\overrightarrow{SM}$|•|$\overrightarrow{SN}$|=$\sqrt{169-48co{s}^{2}(θ+\frac{π}{6})}$∈[11,13]…(12分)
所以cos∠MSN∈[$\frac{11}{13}$,1],
∴∠MSN<60°恒成立
故在彩杆转动的任意时刻,摄影者都可以将彩杆全部摄入画面
点评 本题考查的是解三角形的应用,解题的关键是准确理解基本概念:仰角俯角问题,熟知锐角三角函数的定义及正弦、余弦定理.


| A. | 0 | B. | 3 | C. | 6 | D. | 8 |
| A. | $\frac{12}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
| A. | $\frac{4π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
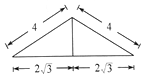
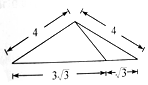
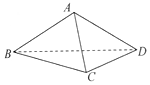 如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )
如图,在三棱锥A-BCD中,侧面ABD⊥底面BCD,BC⊥CD,AB=AD=4,BC=6,BD=4$\sqrt{3}$,该三棱锥三视图的正视图为( )

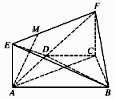 如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.
如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.