题目内容
3.已知变量x,y满足约束条件$\left\{\begin{array}{l}x-y≥1\\ x+y≥1\\ 2x-y≤4\end{array}\right.$,则$z=\frac{{{y^2}+\frac{1}{3}xy+{x^2}}}{x^2}$的最大值与最小值的比值 为( )| A. | $\frac{12}{7}$ | B. | $\frac{77}{75}$ | C. | $\frac{95}{36}$ | D. | $\frac{125}{77}$ |
分析 由约束条件作出可行域,数形结合求出$\frac{y}{x}$的范围,然后利用配方法求出$z=\frac{{{y^2}+\frac{1}{3}xy+{x^2}}}{x^2}$的最大值与最小值得答案.
解答 解:由约束条件$\left\{\begin{array}{l}x-y≥1\\ x+y≥1\\ 2x-y≤4\end{array}\right.$作出可行域如图,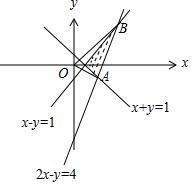
联立$\left\{\begin{array}{l}{x+y=1}\\{2x-y=4}\end{array}\right.$,解得A($\frac{5}{3},-\frac{2}{3}$),
联立$\left\{\begin{array}{l}{x-y=1}\\{2x-y=4}\end{array}\right.$,得B(3,2).
∴$\frac{y}{x}∈$($-\frac{2}{5},\frac{2}{3}$),
则$z=\frac{{{y^2}+\frac{1}{3}xy+{x^2}}}{x^2}$=$(\frac{y}{x})^{2}+\frac{1}{3}(\frac{y}{x})+1$=$(\frac{y}{x}+\frac{1}{6})^{2}+\frac{35}{36}$.
∴当$\frac{y}{x}=-\frac{1}{6}$时,${z}_{min}=\frac{35}{36}$,当$\frac{y}{x}=\frac{2}{3}$时,${z}_{max}=\frac{60}{36}$.
∴$z=\frac{{{y^2}+\frac{1}{3}xy+{x^2}}}{x^2}$的最大值与最小值的比值为$\frac{60}{35}=\frac{12}{7}$.
故选:A.
点评 本题考查简单的线性规划,考查数形结合的解题思想方法,训练了利用配方法求函数的最值,是中档题.

| A. | $\frac{1}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
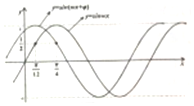
| A. | 沿x轴向左平移$\frac{π}{6}$个单位 | B. | 沿x轴向左平移$\frac{π}{3}$个单位 | ||
| C. | 沿x轴向右平移$\frac{π}{6}$个单位 | D. | 沿x轴向右平移$\frac{π}{6}$个单位 |
| A. | 30 | B. | 40 | C. | 50 | D. | 以上都不正确 |
| A. | 19 | B. | 20 | C. | 21 | D. | 22 |
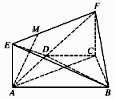 如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.
如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.