题目内容
锐角△ABC中,边a,b是方程x2-2
x+2=0的两根,角A,B满足sinAcosB+cosAsinB=
,求:
(Ⅰ)角C的大小;
(Ⅱ)边c的长度及△ABC的面积.
| 3 |
| ||
| 2 |
(Ⅰ)角C的大小;
(Ⅱ)边c的长度及△ABC的面积.
考点:正弦定理,余弦定理
专题:计算题,解三角形
分析:(Ⅰ)由sinAcosB+cosAsinB=
,得sin(A+B)=
,由△ABC为锐角三角形,可得A+B=120°,即可求∠C.
(Ⅱ)由题意a+b=2
,ab=2,由余弦定理可求得c2=6,从而可求边c的长度及△ABC的面积.
| ||
| 2 |
| ||
| 2 |
(Ⅱ)由题意a+b=2
| 3 |
解答:
解:(Ⅰ)由sinAcosB+cosAsinB=
,得sin(A+B)=
…2分
∵△ABC为锐角三角形,
∴A+B=120°,
∴∠C=60°…5分
(Ⅱ)∵a,b是方程x2-2
x+2=0的两根,
∴a+b=2
,ab=2…7分
∴c2=a2+b2-2abcosC=(a+b)2-3ab=12-6=6…9分
∴c=
…10分
∴S△ABC=
absinC=
×2×
=
…12分
| ||
| 2 |
| ||
| 2 |
∵△ABC为锐角三角形,
∴A+B=120°,
∴∠C=60°…5分
(Ⅱ)∵a,b是方程x2-2
| 3 |
∴a+b=2
| 3 |
∴c2=a2+b2-2abcosC=(a+b)2-3ab=12-6=6…9分
∴c=
| 6 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
点评:本题主要考查了余弦定理、三角形面积公式、三角函数恒等变换的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知(1+bi)2=2i(b∈R,i是虚数单位),则b=( )
| A、2 | B、1 | C、±1 | D、1或2 |
已知等差数列{an}的前n项和为Sn,a1=1,S5=15,则数列{
}的前10项和为( )
| 1 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知过点A(-2,m),B(m,4)的直线与直线2x+y-1=0平行,则m的值为( )
| A、0 | B、2 | C、-8 | D、10 |
已知函数f(x)=sinxcosx+
cos2x-
.
(1)求函数f(x)的最小正周期及单调递减区间;
(2)如果△ABC的角A,B,C所对的边为a,b,c,且满足b2=ac,试求f(B)的取值范围.
| 3 |
| ||
| 2 |
(1)求函数f(x)的最小正周期及单调递减区间;
(2)如果△ABC的角A,B,C所对的边为a,b,c,且满足b2=ac,试求f(B)的取值范围.
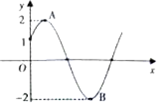 若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤
若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤| π |
| 2 |
A、ω=
| ||||
B、ω=
| ||||
C、ω=
| ||||
D、ω=
|
 如图,在正方形OABC内任取一点,取到函数y=
如图,在正方形OABC内任取一点,取到函数y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|