题目内容
已知曲线C:
(参数θ∈[0,2π),直线l:x+2y=10.
(1)设点P是曲线C上任一点,求P到直线l的距离的最大值和最小值;
(2)以原点O为极点,x轴正半轴为极轴,建立极坐标系,取相同的长度单位,求C与直线l的极坐标方程.
|
(1)设点P是曲线C上任一点,求P到直线l的距离的最大值和最小值;
(2)以原点O为极点,x轴正半轴为极轴,建立极坐标系,取相同的长度单位,求C与直线l的极坐标方程.
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)由曲线C:
(参数θ∈[0,2π),利用sin2θ+cos2θ=1消去参数θ,即可得出直角坐标方程.设与此椭圆相切且与直线l:x+2y=10平行的直线为x+2y+m=0.与椭圆方程联立化为25y2+16my+4m2-36=0,令△=0,解得m.利用平行线之间的距离公式即可得出.
(2)把
分别代入曲线C与直线l:x+2y=10的方程,即可得出极坐标方程.
|
(2)把
|
解答:
解:(1)由曲线C:
(参数θ∈[0,2π),消去参数θ,化为
+
=1.
设与此椭圆相切且与直线l:x+2y=10平行的直线为x+2y+m=0.
联立
,化为25y2+16my+4m2-36=0,
令△=256m2-100(4m2-36)=0,
解得m=±5.
∴直线l:x+2y=10与两条平行切线x+2y±5=0的距离分别:
,3
.
∴P到直线l的距离的最大值和最小值分别为:3
,
;
(2)把
分别代入曲线C
+
=1,直线l:x+2y=10的方程,
可得极坐标方程:4ρ2cos2θ+9ρ2sin2θ=36,ρcosθ+2ρsinθ-10=0.
|
| x2 |
| 9 |
| y2 |
| 4 |
设与此椭圆相切且与直线l:x+2y=10平行的直线为x+2y+m=0.
联立
|
令△=256m2-100(4m2-36)=0,
解得m=±5.
∴直线l:x+2y=10与两条平行切线x+2y±5=0的距离分别:
| 5 |
| 5 |
∴P到直线l的距离的最大值和最小值分别为:3
| 5 |
| 5 |
(2)把
|
| x2 |
| 9 |
| y2 |
| 4 |
可得极坐标方程:4ρ2cos2θ+9ρ2sin2θ=36,ρcosθ+2ρsinθ-10=0.
点评:本题考查了把极坐标化为直角坐标、参数方程化为普通方程、点到直线的距离公式、平行线之间的距离公式、直线与椭圆的位置关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设a=sin(π-
),函数f(x)=
,则f(log2
)的值等于( )
| π |
| 6 |
|
| 1 |
| 6 |
A、
| ||
| B、4 | ||
C、
| ||
| D、6 |
已知(1+bi)2=2i(b∈R,i是虚数单位),则b=( )
| A、2 | B、1 | C、±1 | D、1或2 |
已知一个算法,其流程图如图所示,则输出结果是( )


| A、9 | B、27 | C、81 | D、243 |
已知等差数列{an}的前n项和为Sn,a1=1,S5=15,则数列{
}的前10项和为( )
| 1 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
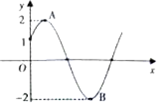 若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤
若函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤| π |
| 2 |
A、ω=
| ||||
B、ω=
| ||||
C、ω=
| ||||
D、ω=
|