题目内容
对一个样本容量为100的数据分组，各组的频数如表：
估计小于29的数据大约占总体的（ ）
| 区间 | [17，19） | [19，21） | [21，23） | [23，25） | [25，27） | [27，29） | [29，31） | [31，33] |
| 频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
| A、42% | B、58% |
| C、40% | D、16% |
考点：用样本的数字特征估计总体的数字特征
专题：概率与统计
分析：由表格可以看出，样本在区间[17，29）上的数据个数，样本容量为100，进而得到小于29的数据大约占总体的42%．
解答：
解：由表格可以看出，样本在区间[17，29）上的数据个数为1+1+3+3+18+16=42个数据，
∵样本容量为100，
∴样本在区间[17，29）上的频率为
，
则估计小于29的数据大约占总体的42%，
故选：A．
∵样本容量为100，
∴样本在区间[17，29）上的频率为
| 42 |
| 100 |
则估计小于29的数据大约占总体的42%，
故选：A．
点评：本题考查频率的求法，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
在数列{an}中，an+1=
（n∈N+）且a7=
，则a5=（ ）
| 2an |
| 2+an |
| 1 |
| 2 |
| A、1 | ||
B、
| ||
C、
| ||
| D、-1 |
与57°角的终边相同的角的集合是（ ）
| A、{α|α=57°+k•360°，k∈Z} |
| B、{α|α=-157°+k•360°，k∈Z} |
| C、{α|α=33°+k•360°，k∈Z} |
| D、{α|α=-33°+k•360°，k∈Z} |
已知f（x）=cos(ωx+
)的图象与y=1的图象的两相邻交点间的距离为π，要得到y=f（x）的图象，只需把y=sinωx的图象（ ）
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
设集合A={x|
＜x＜2}，B={x|x2＜1}，则A∪B=（ ）
| 1 |
| 2 |
| A、{x|1＜x＜2} | ||
| B、{x|-1＜x＜2} | ||
C、{x|
| ||
| D、{x|-1＜x＜1} |
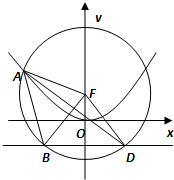设抛物线C：x2=2py（p＞0）的焦点为F，准线为l，A为C上一点，已知以F为圆心，FA为半径的圆F交l于B，D两点．若∠BFD=90°，△ABD的面积为4