题目内容
3.已知a,b是两个任意的正数,且满足a+b=2,则a•b的最大值为1.分析 由题意和基本不等式可得a•b≤($\frac{a+b}{2}$)2=1,验证等号成立即可.
解答 解:∵a,b是两个任意的正数,且满足a+b=2,
∴由基本不等式可得a•b≤($\frac{a+b}{2}$)2=1,
当且仅当a=b=1时取等号,
故所求的最大值为1,
故答案为:1.
点评 本题考查基本不等式求最值,属基础题.

练习册系列答案
相关题目
14.在0°-360°的范围内,与-510°终边相同的角是( )
| A. | 330° | B. | 210° | C. | 150° | D. | 30° |
15.函数f(x)=x3-15x的某个零点所在的一个区间是( )
| A. | (-2,0) | B. | (-1,1) | C. | (0,2) | D. | (1,3) |
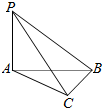 如图,Rt△ABC中,∠ACB=90°,∠BAC=45°,PA⊥平面ABC,且PA=BC=1,则二面角A-PB-C的平面角是60°.
如图,Rt△ABC中,∠ACB=90°,∠BAC=45°,PA⊥平面ABC,且PA=BC=1,则二面角A-PB-C的平面角是60°.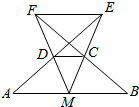 已知:如图,AB∥CD,M是AB的中点,MC的延长线与AD的延长线交于点E,MD的延长线与BC的延长线交于点F.求证:EF∥AB.
已知:如图,AB∥CD,M是AB的中点,MC的延长线与AD的延长线交于点E,MD的延长线与BC的延长线交于点F.求证:EF∥AB.