题目内容
7.cos$(\frac{-13π}{4})$的值为( )| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 把原式中的角度变形,利用诱导公式化简即可得到答案.
解答 解:cos$(\frac{-13π}{4})$=cos(-4π+$\frac{3π}{4}$)=cos$\frac{3π}{4}$=cos(π-$\frac{π}{4}$)=-$\frac{\sqrt{2}}{2}$.
故选:A.
点评 本题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键,是基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
18.已知抛物线的方程为y=2px2且过点(1,4),则抛物线的焦点坐标为( )
| A. | (1,0) | B. | $(\frac{1}{16},0)$ | C. | $(0,\frac{1}{16})$ | D. | (0,1) |
15.已知函数f(x)=x2+mx+n,其中1≤m≤3,0≤n≤4,记函数f(x)满足条件$\left\{\begin{array}{l}f(2)≤12\\ f(-1)≤3\end{array}\right.$的事件为A,则事件A发生的概率为( )
| A. | $\frac{5}{8}$ | B. | $\frac{13}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
2.实轴长为4$\sqrt{5}$,且焦点为(±5,0)的双曲线的标准方式为( )
| A. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{y}^{2}}{20}$-$\frac{{x}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{25}$=1 |
19.f(x)=2x-cosx在(-∞,+∞)上( )
| A. | 有最大值 | B. | 是减函数 | C. | 是增函数 | D. | 有最小值 |
16.自点 A(-3,4)作圆(x-2)2+(y-3)2=1的切线,则A到切点的距离为( )
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{10}$ | D. | 5 |
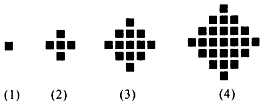 某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
某民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.先按照同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.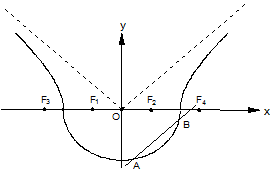 如图,曲线Г由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)和曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点,
如图,曲线Г由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)和曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点,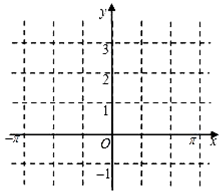 已知函数f(x)=2sin(2ωx+$\frac{π}{6}$)+1(其中0<ω<1),若点(-$\frac{π}{6}$,1)是函数f(x)图象的一个对称中心,
已知函数f(x)=2sin(2ωx+$\frac{π}{6}$)+1(其中0<ω<1),若点(-$\frac{π}{6}$,1)是函数f(x)图象的一个对称中心,