题目内容
4.已知等比数列{an}满足:${a_1}=\frac{1}{2},2{a_3}={a_2}$(1)求数列{an}的通项公式;
(2)若等差数列{bn}的前n项和为Sn,满足b1=1,S3=b2+4,求数列{an•bn}的前n项和Tn.
分析 (1)求得等比数列的公比q,由等比数列的通项公式计算即可得到;
(2)求出等差数列{bn}的公差d,运用等差数列的通项公式,可得bn,求得an•bn=n•($\frac{1}{2}$)n,再由数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.
解答 解:(1)等比数列{an}满足:${a_1}=\frac{1}{2},2{a_3}={a_2}$,
可得公比q=$\frac{{a}_{3}}{{a}_{2}}$=$\frac{1}{2}$,
数列{an}的通项公式为an=a1qn-1=($\frac{1}{2}$)n;
(2)等差数列{bn}的前n项和为Sn,满足b1=1,S3=b2+4,
设公差为d,则3+3d=5+d,解得d=1,
则bn=b1+(n-1)d=n,
an•bn=n•($\frac{1}{2}$)n,
前n项和Tn=1•($\frac{1}{2}$)+2•($\frac{1}{2}$)2+…+n•($\frac{1}{2}$)n,
$\frac{1}{2}$Tn=1•($\frac{1}{2}$)2+2•($\frac{1}{2}$)3+…+n•($\frac{1}{2}$)n+1,
两式相减可得,$\frac{1}{2}$Tn=$\frac{1}{2}$+($\frac{1}{2}$)2+($\frac{1}{2}$)3+…+($\frac{1}{2}$)n-n•($\frac{1}{2}$)n+1
=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-n•($\frac{1}{2}$)n+1,
化简可得Tn=2-(n+2)•($\frac{1}{2}$)n.
点评 本题考查等比数列和等差数列的通项公式和求和公式的运用,考查数列的求和方法:错位相减法,考查化简整理的运算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $\frac{5}{8}$ | B. | $\frac{13}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
| A. | 有最大值 | B. | 是减函数 | C. | 是增函数 | D. | 有最小值 |
| A. | cos(2x+y) | B. | cosy | C. | sin(2x+y) | D. | siny |
| A. | $\sqrt{5}$ | B. | 3 | C. | $\sqrt{10}$ | D. | 5 |
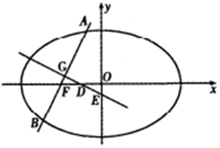 如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),过点F的直线交椭圆于A,B两点,当直线AB经过椭圆的一个顶点时,其倾斜角恰为60°.
如图,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点为F(-c,0),过点F的直线交椭圆于A,B两点,当直线AB经过椭圆的一个顶点时,其倾斜角恰为60°.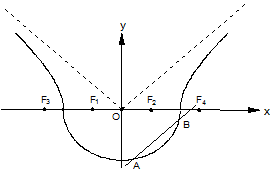 如图,曲线Г由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)和曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点,
如图,曲线Г由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)和曲线C2:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y>0)组成,其中点F1,F2为曲线C1所在圆锥曲线的焦点,点F3,F4为曲线C2所在圆锥曲线的焦点, 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2$\sqrt{2}$,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2$\sqrt{2}$,∠BAC=90°,O为BC中点.