题目内容
13.已知点P(4,-3)在角φ的终边上,函数f(x)=sin(ωx+φ)(ω>0)图象上与y轴最近的两个对称中心间的距离为$\frac{π}{2}$,则f($\frac{π}{8}$)的值为( )| A. | $\frac{7\sqrt{2}}{10}$ | B. | -$\frac{7\sqrt{2}}{10}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | -$\frac{\sqrt{2}}{10}$ |
分析 根据点P在角φ的终边上求出sinφ、cosφ,再根据函数f(x)图象上与y轴最近的两个对称中心间的距离求出T,计算ω的值,从而求出f($\frac{π}{8}$)即可.
解答 解:∵点P(4,-3)在角φ的终边上,
∴sinφ=-$\frac{3}{5}$,cosφ=$\frac{4}{5}$;
由函数f(x)图象上与y轴最近的两个对称中心间的距离为$\frac{π}{2}$,
得T=2×$\frac{π}{2}$=π,
∴ω=$\frac{2π}{T}$=2;
∴f($\frac{π}{8}$)=sin(2×$\frac{π}{8}$+φ)
=sin$\frac{π}{4}$cosφ+cos$\frac{π}{4}$sinφ
=$\frac{\sqrt{2}}{2}$×$\frac{4}{5}$+$\frac{\sqrt{2}}{2}$×(-$\frac{3}{5}$)
=$\frac{\sqrt{2}}{10}$.
故选:C.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了求三角函数值的问题,是基础题.

练习册系列答案
相关题目
9.命题“?n∈N,f(n)∉N且f(n)≤n”的否定形式是( )
| A. | ?n∈N,f(n)∈N且f(n)>n | B. | ?n0∈N,f(n0)∈N且f(n0)>n0 | ||
| C. | ?n∈N,f(n)∈N或f(n)>n | D. | ?n0∈N,f(n0)∈N或f(n0)>n0 |
10.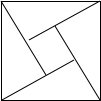 在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
 在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )
在如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角α=$\frac{π}{6}$,现在向该大正方形区域内随机地投掷一枚飞镖,则飞镖落在小正方形内的概率是( )| A. | 1-$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{4-\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
18.已知函数f(x)=2sin(ωx+$\frac{π}{4}$)(ω>0)的图象在区间[0,1]上恰有3个最高点,则ω的取值范围为( )
| A. | [$\frac{19π}{4}$,$\frac{27π}{4}$) | B. | [$\frac{9π}{2}$,$\frac{13π}{2}$) | C. | [$\frac{17π}{4}$,$\frac{25π}{4}$) | D. | [4π,6π) |
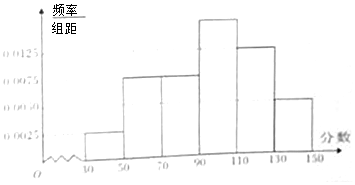 某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图:
某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图: